В Камаев - Технологии программирования

dl: Real; {Значение дискриминанта}

begin

ClrScr; { Очистка экрана }

{Вывод информации о назначении программы}

WriteLn ('Программа решения квадратного уравнения');

WriteLn ( 'вида a*x*x + b*x + c = 0 с произвольными', 'значениями');

WriteLn ('коэффициентов a, b, c типа ', 'вещественный');

WriteLn

{Ввод значений коэффициентов a, b, c}

Write ('Укажите значение коэффициента а = ');

ReadLn(a); { Ввод а }

Write ('Укажите значение коэффициента b = ');

ReadLn(b); { Ввод b}

Write ('Укажите значение коэффициента с = ');

ReadLn(c); { Ввод с }

{ Вывод проверочно-протокольной информации

о введенных значениях коэффициентов a, b, c }

WriteLn;

WriteLn ('Решается квадратное уравнение');

WriteLn (а:10:4, '*x*x + ', b:10:4, '*x + ', с:10:4, ' = 0:');

{ Само решение квадратного уравнения }

if (Abs (a) > 1e-6)

then

begin

{ Продолжение решения с вычислением дискриминанта }

{ Вычисление дискриминанта квадратного уравнения }

d:= Sqr(b) — 4.0*а*с;

{ Решение уравнения }

if d > 1e-6

then

begin

{ Расчет двух различных корней }

x1:= (-b) — Sqrt(d)/(2.0*a);

х2:= (-b) + Sqrt(d)/(2.0*a);

Write ('два различных корня x1 = ', x1:10:4);

WriteLn (' х2 = ', х2:10:4);

end;

if ((d >= -1e-6) and (d <= 1e-6))

then

WriteLn ('два равных корня х = ', (-b)/(2.0*a):10:4);

if d < -1e-6 then

WriteLn ('уравнение не имеет решения');

end;

if ((Abs(a) <= 1e-6) and (Abs(b) > 1e-6))

then

begin

{ Решение линейного уравнения }

x1:= — c/b;

WriteLn ('уравнение линейное х = ', x1:10:4);

end;

if ((Abs(a) <= 1e-6) and (Abs(b) <= 1e-6 and (Abs(c) > 1e-6))

then

WriteLn ('Нет решения');

if ((Abs(a) <= 1e-6 and (Abs(b) <= 1e-6 and (Abs(c) <= 1e-6))

then

begin

Write ('Бесчисленное множество решений',

'уравне');

WriteLn ('ния (корни — любые числа)');

end;

WriteLn;

Write ('Для завершения программы нажмите');

WriteLn ('любую клавишу…');

repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши }

end.

В качестве примера приводится учебная работа, выполненная одним из обучаемых. Работа была оформлена на отдельных листах формата A4. Курсивом выделены пояснения авторов учебника, которые были дополнительно ими внесены в текст работы.

Страница 1 (без нумерации) представляет собой титульный лист с наименованием: "ЗАДАНИЕ НА СОСТАВЛЕНИЕ СТРУКТУРИРОВАННОГО АЛГОРИТМА".

Страница 2 содержит постановку задачи и набор тестов, составленных до разработки алгоритма процесса.

Шаг 1. ПОСТАНОВКА ЗАДАЧИ

Составить алгоритм умножения двух положительных чисел с произвольным (до ста) количеством цифр. Цифры сомножителей и результата должны находиться в одномерных массивах. Разрядность результата не должна превышать 100 цифр.

Шаг 2. НАБОР ТЕСТОВ, СОСТАВЛЕННЫХ ДО РАЗРАБОТКИ АЛГОРИТМА ПРОЦЕССА

Пусть предельная разрядность сомножителей равна трем цифрам, а результата — четырем. Аналогично приведенному образцу умножения чисел 391*56 = 21896 (переполнение) были составлены тесты: 23*132 = 3036; 111*11 = 1221; 999*99 = 98901 (переполнение); 00*000 = 0; 1*0 = 0.

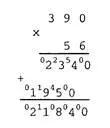
Алгоритм умножения обычно изучался в младших классах школы по маршрутному описанию процесса счета. Из-за теоретической огромности числа маршрутов большинство со школьной скамьи не знает процесса умножения при нулевых сомножителях!

Страница 3 содержит результаты анализа выходной и входной информации вычислительного процесса со структурами данных. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.

Шаг 3. АНАЛИЗ ВЫХОДНОЙ И ВХОДНОЙ ИНФОРМАЦИИ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Анализ выходной и входной информации начинается с рассмотрения модели "черного" ящика, показанной на рис. 5.3.

Program MultNumbers;

{Расчет произведения двух чисел}

uses

Crt;

const

Digits = 100; {Число цифр в числах}

type

TNumber = record

D: array[1..Digits] of Byte;

{B D[1] находится младший разряд числа}

N: word; {Число разрядов в числе от 1 до Digits}

end;

var

C1: TNumber; {Первый сомножитель}

C2: TNumber; {Второй сомножитель}

R: TNumber; {Результат умножения}

Error: boolean; {True — ошибка переполнения}

Макет экрана со строками диалога программы приведен на рис. 5.17. Вместо трех последних строк возможен вывод: "Ошибка переполнения".

Страница 4 содержит наглядное изображение процесса преобразования входных данных обобщающего теста или тестов в выходные данные со всеми внутренними данными и/или трассу выполнения обобщающего теста или тестов. Обобщающий тест или тесты составляются на основе тестов страницы 2 и при минимальном количестве тестов охватывает все маршруты процесса вычислений. Наглядность изображения изменений всех данных способствует упрощению процесса разработки алгоритма. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.

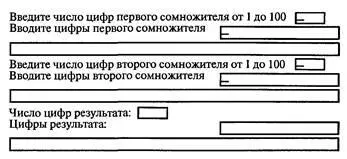
Рис. 5.17. Макет экрана со строками диалога программы

Шаг 4. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ПРОЦЕССА ПРЕОБРАЗОВАНИЯ ВХОДНЫХ ДАННЫХ ОБОБЩАЮЩЕГО ТЕСТА В ВЫХОДНЫЕ

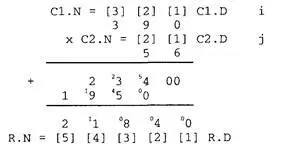
Вводим описание новых внутренних переменных:

var {Рабочие переменные}

i, j: word;

На первый взгляд, кажется, что необходимо ввести переменное количество промежуточных массивов (в зависимости от количества цифр второго сомножителя) для запоминания продукта умножения первого сомножителя на очередную цифру второго сомножителя. Однако внимательный анализ структур данных позволяет найти иной способ выполнения расчетов. При этом способе сначала обнуляется результат. Далее результат последовательно увеличивается на сдвинутый на разряд влево продукт умножения первого сомножителя на очередную цифру второго сомножителя. Переоформляем наглядное изображение процесса преобразования входных данных обобщающего теста.

На странице 4 или следующей иногда полезно поместить описание алгоритма в обыденном неструктурированном понимании.