В Камаев - Технологии программирования
- Название:Технологии программирования
- Автор:
- Жанр:
- Издательство:Издательство «Высшая школа»
- Год:2006
- Город:Москва
- ISBN:5-06-004870-5
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
В Камаев - Технологии программирования краткое содержание
Второе издание (1-е — 2005 г.) дополнено главами по структуре данных и основам инженерии создания программ.
Для студентов вузов, обучающихся по направлению «Информатика».
Технологии программирования - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Первоначально алгоритм должен представлять одну типовую структуру СЛЕДОВАНИЕ (одно действие со смыслом выполнить все действия программы, например, программа начисления заработанной платы, но не программа начисления заработанной платы и/или решения квадратного уравнения).
Глядя на тесты и изображение модели "черного ящика" (см. рис. 5.3), детализируем весь алгоритм как одно СЛЕДОВАНИЕ (последовательно выполняемое действие) в порядке: а) предварительная запись смысла действия "черного ящика"; б) выходная и/или выводимая информация; в) входная и/или вводимая информация; г) определяется действие в "черном ящике" (одно предложение).
При разработке алгоритмов программ входная, промежуточная и выходная информации характеризуются структурой данных. Важным являются порядок размещения значений в массивах, имена и значения констант описания размерностей массива, имена и значения переменных, характеризующие текущие значения используемого размера массива, имя и порядок изменения переменной индекса текущего элемента массива. Форма вводимой и выводимой на экран или печать информации может быть показана макетами экранов или документов.
Первичные тестовые примеры должны включать как обычные, так и стрессовые наборы тестовых входных данных. Каждый стрессовый набор тестовых данных предназначен для выявления реакции в особых случаях. Например: неверных действий пользователя, деления на ноль, выхода значения за допустимые границы и т. д. Любой набор тестовых данных должен содержать описание результата.
Исследуя "черный ящик" применительно к решению квадратного уравнения, можем записать предварительный комментарий сути всех действий программы: "Программа решения квадратного уравнения вида a*x*x + b*x + c = 0".
Далее выясняется, что еще не выявлена выходная информация "черного ящика", поэтому необходимо перейти к подготовке тестов, что поможет продолжить работу с "черным ящиком". В данном конкретном случае подготовить тесты поможет анализ задачи.
Итак, пусть известна "школьная" формула решения квадратного уравнения вида ax 2+ bx + с = 0.
Известно также, что первоначально надо вычислить дискриминант уравнения D:
D = b 2— 4ac.
Даже если забыли о случае отрицательности дискриминанта — ничего страшного нет. Записываем формулу решения:
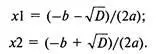
Нам известно, что если D < 0, то из отрицательного числа нельзя извлекать квадратный корень. Поэтому вспоминаем, что при отрицательном дискриминанте нет корней. Еще обнаруживаем факт особого случая, которому соответствует факт при D = 0 наличия двух равных корней. Еще известно, что делить на ноль нельзя, а при a = 0 имеем именно этот случай. В этом случае исходное квадратное уравнение превращается в линейное уравнение:
bx + c = 0.
Решение получившегося уравнения будет следующим:
x = (—c)/b.
Это решение возможно лишь в случае a = 0 и (одновременно) b ≠ 0. В случае a = 0 и (одновременно) b = 0 и (одновременно) c ≠ 0 линейное уравнение не имеет решения.
Анализируя исходное уравнение, выясняем, что в случае a = 0 и (одновременно) b = 0 и (одновременно) c = 0 уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа).
Составим наглядную таблицу правил решения квадратного уравнения (табл. 5.3).
Таблица 5.3
Наглядная таблица правил решения квадратного уравнения
| № п/п | а | b | с | d | Вариант решения |
| 1 | a ≠ 0 | Любое | Любое | d > 0 | Два различных корня |
| 2 | a ≠ 0 | Любое | Любое | d = 0 | Два равных корня |
| 3 | a ≠ 0 | Любое | Любое | d < 0 | Нет решения |
| 4 | а = 0 | b ≠ 0 | Любое | Нет | Есть корень линейного уравнения |
| 5 | а = 0 | b = 0 | c ≠ 0 | Нет | Нет решения |
| 6 | а = 0 | b = 0 | с = 0 | Нет | Бесчисленное множество решений |
В табл. 5.3 нет сочетаний значений, которые еще не выявлены. Теперь можно определить выходную информацию "черного ящика", которая выдается в пяти вариантах:
1) уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа);
2) значения двух различных корней x1 и x2;
3) значения двух равных корней в виде x1 и дополняющей надписи о двух равных корнях;
4) надпись нет решения;
5) значение одного корня x1 с надписью, что уравнение является линейным.
Тип переменных, в которых размещаются выходные значения корней x1 и x2, — вещественный (Real). Теперь определяем входную информацию. Из исходного уравнения следует, что входной информацией являются значения трех коэффициентов a, b, c типа вещественный (Real). В ходе анализа формул было установлено, что значения трех коэффициентов a, b, c могут принимать любые значения, что было не очевидно до анализа формул решения уравнения (например, случай a = 0).
Имена переменных будут достаточно мнемоничны, если придерживаться принятых в математике обозначений.
Окончательный комментарий сути действий всей программы: "Программа решения квадратного уравнения a*x*x + b*x + c = 0 с произвольными значениями коэффициентов a, b, c типа вещественный". Факт произвольности значений коэффициентов a, b, c на этапе предварительного выявления сути действия "черного ящика" еще не был выявлен.
Наконец, готовим тестовые примеры.
Совокупность тестов для всех выявленных случаев решения квадратного уравнения:
1) при a = 0, b = 0, c = 0 бесчисленное множество решений (корни x1 и x2 — любые числа);
2) при a = 2, b = 3, c = —2 значения двух различных корней x1 = —2 и x2 = 0,5;
3) при a = 1, b = 4, c = 4 значения двух равных корней в виде x1 = x2 = —2 и вывод дополняющей надписи о двух равных корнях;
4) при а = 2, b = 5, с = 4 вывод надписи "нет решения";
5) при a = 0, b = 2, c = —8 значение одного корня x1 = 4 с надписью, что уравнение является линейным;
6) при a = 0, b = 0, c = 2 вывод надписи "нет решения". Теперь можно сразу написать фрагмент программы, соответствующий проделанной работе:
Program Kvadrat;
{ Программа решения квадратного уравнения
вида a*x*x + b*x + c = 0 с произвольными
значениями коэффициентов a, b, c типа
вещественный }
Uses
Crt, Dos;
Var
a, b, c: Real; {Коэффициенты квадратного уравнения}
xl, x2: Real; {Корни квадратного уравнения}
begin
end.
Путем компиляции фрагмента программы на компьютере можно проверить корректность синтаксиса. Теперь подготовим макет изображения экрана монитора (рис. 5.16). На макете изображения экрана монитора символами □ отмечены поля ввода информации, а символами — поля вывода информации.
Обычно выводимая на экран информация не содержит имен переменных, но в данном случае принятые в математике имена целесообразно отобразить на экране.
Читать дальшеИнтервал:
Закладка:









