В Камаев - Технологии программирования

Ниже приведен пример описания программы "Редактор текстов", составленный одним из обучаемых. В примере приводится сначала внешняя функциональная спецификация, а затем внутренняя спецификация.

Программа "Редактор текстов" предназначена для создания новых и корректировки существующих текстовых файлов MS DOS в диалоговом (пользователь-ЭВМ) режиме работы. ЭВМ формирует экран с окном, в котором отображен участок текста из текстового файла (макет экрана соответствует внутреннему редактору программы Norton Commander). Пользователю обеспечивается возможность вставки в текст в окне экрана любого символа клавиатуры за символом, отмеченным на экране курсором. Исключение составляет ряд символов, которые являются признаками команд управления или незадействованными символами (приводится список символов). После подачи пользователем команды записи все изменения текста, осуществленные пользователем, записываются в файл.

Основной принцип работы редактора текстов состоит в переносе строк текста из необходимых участков файла сначала в буферный массив памяти длиной в 65535 байт (символов) с дальнейшим копированием необходимых строк из буферного массива в окно экрана.

Запуск программы осуществляется командой с указанием имени редактируемого файла. Далее, пока не будет указано корректное имя файла, может начать многократно выполняться алгоритм "Запрос пользователя на ввод или корректировку имени файла".

Затем задаются начальные значения структурированной переменной "Система координат", в которой имеются поля: "Положение курсора относительно файла"; "Положение курсора относительно буферного окна редактора"; "Положение буферного окна редактора относительно файла".

После осуществляется очистка буферного массива редактора строковых переменных из 5 * 23 = 115 строк длиной по 225 символов.

Далее при параметре "Первая строка файла" выполняется алгоритм "Загрузка строк файла, начиная с указанной строки в буферный массив редактора". Потом до подачи пользователем одной из команд завершения редактирования с сохранением информации (или без сохранения) выполняется главный цикл программы. Наконец, если была дана команда завершения с сохранением информации, то информация из буферного массива переписывается в файл. Выполнение программы завершается очисткой экрана.

Контроль имени редактируемого файла состоит в следующем. Если файл с указанным именем отсутствует на диске, то выводится предупреждающее сообщение о создании нового "пустого" файла. Если пользователь не указал имя редактируемого файла или отказался работать с созданным "пустым" файлом, то происходит аварийное завершение программы с пояснением причины завершения.

Внутри главного цикла программы выполняется ряд из трех последовательных действий. "Алгоритм отображение" отображает на экране 23 строки текста из буферного массива, начиная с заданной строки. Далее устанавливается курсор дисплея на заданную позицию экрана. Осуществляется ввод кода нажатой клавиши. Если код нажатой клавиши соответствует управляющей клавише, то выполняется одно из альтернативных действий по выполнению команды, которая соответствует данной клавише. В противном случае осуществляется вставка символа в текст.

Алгоритм Нелдера — Мида является широко известным и применяется в качестве алгоритма прямого поиска локального экстремума вещественных функций от 2 до 6 вещественных переменных.

Следующий абзац содержит фрагмент текста из книги Д. Химмельблау [26], в котором содержится часть описания алгоритма Нелдера — Мида (метода деформируемого многогранника).

В методе Нелдера и Мида минимизируется функция n независимых переменных с использованием n + 1 вершин деформируемого многогранника в E n. Каждая вершина может быть идентифицирована вектором x. Вершина (точка) в E n, в которой значение f(x) максимально, проектируется через центр тяжести (центроид) оставшихся вершин. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f(x) на более "хорошие" точки, пока не будет найден минимум f(x).

Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой в начале координат. Процедура отыскания вершины в E n, в которой f(x) имеет лучшее значение, состоит из следующих операций:

Отражение — проектирование x (k) hчерез центр тяжести в соответствии с соотношением x (k) n+3= x (k) n+2 + α(x (k) n+2 — x (k) h), где α > 0 является коэффициентом отражения; x (k) n+2— центр тяжести, x (k) h— вершина, в которой функция f(x) принимает наибольшее из n + 1 ее значений на k-м этапе.

Растяжение выполняется, если f(x (k) n+3) ≤ f(x (k) i), то вектор (x (k) n+3— x (k) n+2) растягивается в соответствии с соотношением x (k) n+4= x (k) n+2+ γ(x (k) n+3— x (k) n+2), где γ — коэффициент растяжения. Если f(x (k) n+4) < f(x (k) i), то x (k) hзаменяется на x (k) n+4и процедура продолжается с шага 1 (k = k + 1), иначе x (k) nзаменяется на x (k) n+3, процедура продолжается с шага 1 (k = k + 1).

Сжатие — если f(x (k) n+3) > f(x (k) i) для всех i ≠ h, то вектор (x (k) h— x (k) n+2) сжимается в соответствии с формулой x (k) n+5= x (k) n+2+ β(x (k) h— x (k) n+2), где 0 < β < 1 представляет собой коэффициент сжатия. Затем x (k) hзаменяется на x (k) n+5и переходит на шаг 1 (k = k + 1).

Редукция — если f(x (k) n+3) > f(x (k) h), все векторы (x (k) i— x (k) 1), i = 1…n + 1 уменьшаются в 2 раза с отсчетом от x (k) 1в соответствии с формулой x (k) i= x (k) i+ 0,5(x (k) i— x (k) 1), i = 1…n + 1. Затем возвращаемся к шагу 1 для продолжения поиска на k + 1 шаге.

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия среднего квадратичного отклонения функций f(x (k) i) от произвольного малого числа ε.

Химмельблау воспользовался традиционным математическим стилем для изложения описания алгоритма. Алгоритм имеет структуру вида "спагетти", что видно из схемы алгоритма, разработанной автором (рис. 5.15). Схема в виде "спагетти" — это скрытые go to, которые мы обнаруживаем в тексте программы, разработанной автором. Он же приводит графические рисунки принципа расчета точек и графический рисунок последовательности продвижения лучших точек симплекса по шагам метода при решении тестовой задачи. Затратив 11 страниц текста, приведя текст неструктурированной программы на 12 страницах, автор книги [26] так и не сумел понятно описать свой алгоритм.

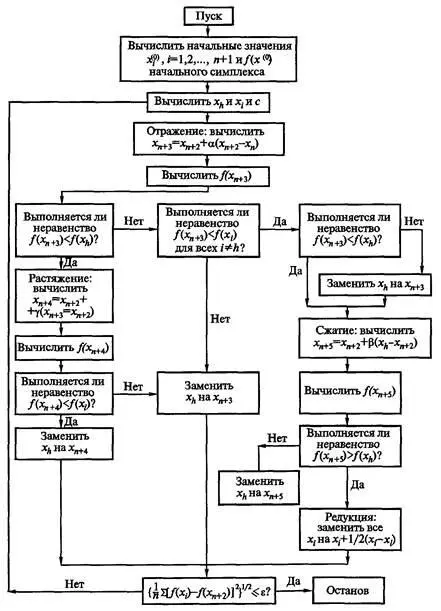
Рис. 5.15. Схема алгоритма, разработанная Д. Химмельблау

Сравните способ подачи описания алгоритма, составленный автором [22], и функциональное описание алгоритма после рефакторинга. Функциональное описание алгоритма приведено ниже.