Тимур Машнин - Объектно-ориентированное программирование на Java. Платформа Java SE

Так как вывод System. out является буферизированным, то есть сообщения сначала помещаются в буфер, прежде они будут выведены в консоль.

А сообщение необработанного исключение выводится через не буферизированный вывод System.err.

Как уже было сказано, каждый оператор try требует наличия либо catch, либо finally.

Поэтому возможна конструкция try – finally.

И блок finally получит управление, даже если try-блок завершится исключением.

И блок finally получит управление, даже если try-блок завершится директивой выхода из метода.

Однако блок finally НЕ будет вызываться, если мы убъем виртуальную машину JVM.

При всем при этом, надо отметить, что блок finally не перехватывает исключение, и программа завершиться ошибкой при возникновении в блоке try исключения.

Исключение перехватывает только блок catch.

Таким образом мы разобрали почти все случаи работы операторов try, catch, throws, throw, и finally.

В некоторых случаях нам нужно выполнять повторные вычисления.

И мы видели циклы for и while, которые выполняют повторные вычисления.

Теперь мы увидим гораздо более мощный механизм повторных вычислений, который называется рекурсией.

Ранее мы определили метод square, который, принимая целое число, возвращает квадрат числа.

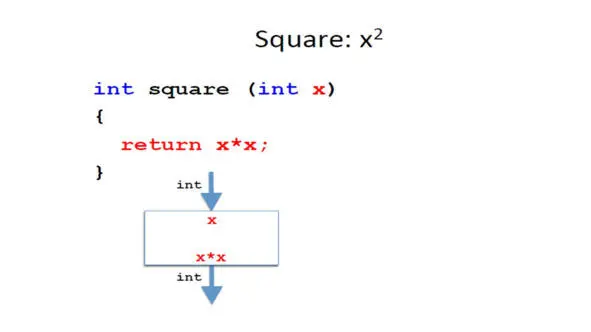
Теперь мы хотели бы определить метод, который возводит в степень.

Мы хотим определить метод, который, учитывая базу x и показатель y, вычисляет x в степени y.

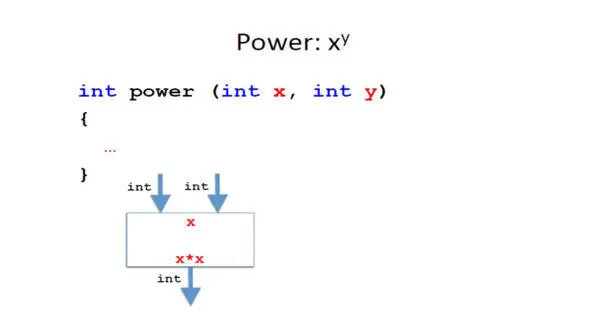
Поэтому, если y равно 2, мы вычисляем квадрат числа, как и раньше.

Вы видите, что в этом методе мы имеем два аргумента, целые числа x и y.

Давайте сначала попытаемся определить этот метод.

Давайте проанализируем несколько случаев.

Если y равно 0, то результат x равен степени 0, т. е. 1.

Если y равно 1, результат будет сразу x.

Если y равно 2, результатом является квадрат x.

Мы можем вызвать метод square, который мы определили ранее.

Если y равно 3, мы имеем x в кубе, предполагая, что у нас есть метод, называемый cube, определенный заранее.

И далее нам понадобятся другие методы для всех различных значений y, которые могут быть приняты.

Теперь мы можем заменить вызовы методов square, cube, и т. д. следующим кодом.

Таким образом, мы будем иметь x умножить на x, x умножить на x умножить на x и т. д.

Сейчас это немного лучше, но все же очень плохо, потому что порождает бесконечный код.

Но мы все же кое-чему научились.

Чтобы вычислить x в степени y, мы должны умножить x y раз.

Но мы должны учитывать, является ли эта процедура применима для всех целых чисел y?

Нет.

Только для y больше или равно 0.

Для отрицательного y нам понадобится другой способ умножения.

Если у нас есть повторное умножение, мы можем использовать цикл.

Вот пример того, как мы можем это сделать.

Мы инициализируем целочисленную переменную z в 1, а затем вводим цикл.

Счетчик i инициализируется 1 и увеличивается на 1 при каждом прогоне цикла.

Этот счетчик отслеживает, сколько х мы умножаем и накапливаем с помощью z.

И мы должны выполнять тело цикла ровно y раз, пока i не станет равен y.

Затем мы выходим и возвращаем накопленное значение в z.

Давайте проанализируем это снова.

x в степени y равно 1, если y равно 0.

А если y строго больше 0, то x в степени y равно x умножить на x в степени y минус 1.

Это то, что в математике называется рекуррентным уравнением.

И мы можем написать это на Java в виде вызова функции power.

Если y равно 0, возвращаем 1.

Иначе, возвращаем x умножить на вызов этой же функции с x и y минус 1.

Таким образом, тот же метод, который мы определили с помощью цикла, может быть определен с помощью рекурсии.

Оба эти способа эквивалентны.

Но рекурсия позволяет записать сложное поведение простым способом, который потребует довольно сложного программирования при использовании циклов.

Рекурсию можно сравнить с матрешкой.

Чтобы понять это вернемся к рекурсивному методу, который мы определили.

И давайте упростим последовательно вызов этого метода для небольшой степени, чтобы увидеть, что происходит.

Начнем с x в 3 степени.

Мы можем заменить вызов метода, используя определение метода.

Таким образом, мы пишем весь код метода, подставляя вместо y 3.

И в этой последовательности выражений мы переходим от вызова метода с параметрами (x, 3) к вызову метода с параметрами (x, 2).

Пишем весь код метода, подставляя вместо y 2.

И в этой последовательности выражений, мы перешли от вызова метода с параметрами (x, 2) к вызову метода с параметрами (x, 1).

И переходим к вызову метода с параметрами (x, 0).

x в степени 0 равно 1.

Теперь нам нужно собрать все вместе.

power (x, 3) равно x умножить на power (x, 2).

А power (x, 2) равно x умножить на power (x, 1).