Тимур Машнин - Объектно-ориентированное программирование на Java. Платформа Java SE

А power (x, 1) равна x умножить на power (x, 0), что равно 1.

Таким образом, мы получаем x умножить на x умножить на x умножить на 1.

Так работает рекурсия – сначала мы спускаемся как по лестнице вниз, а затем поднимаемся опять наверх.

Это изображение коробки с медсестрой, держащей меньшую коробку с тем же изображением.

Так что в теории, могут быть бесконечные медсестры и бесконечные коробки.

Но на практике нет бесконечных коробок, потому что изображение имеет некоторое разрешение, и мы не можем опуститься ниже 1 пикселя.

Таким образом, существует конечное число коробок.

Когда мы что-то вычисляем, мы должны заботиться о том, чтобы не создавать нежелательные бесконечные вычисления, которые нарушают нормальный поток вычислений.

Давайте посмотрим, что произойдет, когда мы что-то неправильно программируем.

Давайте рассмотрим, опять наш рекурсивный метод вычисления степени числа.

И давайте вызовем power (x, -2) для некоторого заданного x.

Для этого мы можем заменить вызов метода кодом.

В результате мы перейдем к вызову метода power (x, -3).

В методе power (x, -3) мы перейдем к вызову метода power (x, -4).

И так далее. Без конца.

Мы получим бесконечные вычисления в теории.

На практике мы получим переполнение в какой-то момент и ошибку.

Что же мы сделали не так?

В этом случае мы не соблюдали комментарий, что y должно быть больше или равно 0.

Поэтому мы должны учитывать две важные вещи.

Во-первых, рекурсия хороша, но мы можем перейти к бесконечным вычислениям.

И во-вторых, чтобы избежать этого, мы должны понять условия, при которых рекурсивный метод фактически завершается.

Может быть определенное количество рекурсивных вызовов, но в какой-то момент, нам нужно достичь не рекурсивного случая.

Поэтому при определении рекурсивного метода, всегда должны быть некоторые значения, для которых метод не вызывается рекурсивно.

Существует два способа чтения и понимания рекурсивных методов.

Один из них – это тот способ, который мы видели.

Другой, математический или нотационный способ, которые мы рассмотрим.

Предположим, нам дана задача написать рекурсивный метод.

Начнем с относительно простой задачи – написать метод на Java для вычисления факториала натурального числа.

В общем случае факториал натурального числа n вычисляется умножением всех натуральных чисел, начиная с 1 до n.

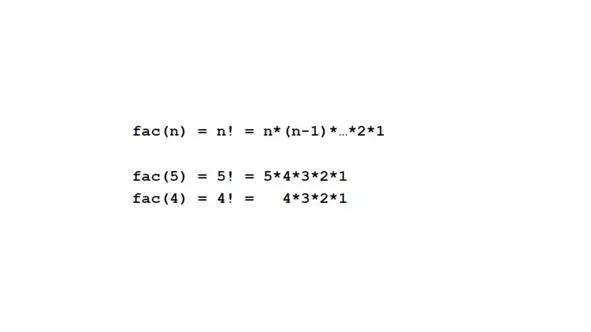
Чтобы решить эту задачу, мы будем использовать следующую стратегию.

Первая часть состоит в том, что мы предполагаем, что задача решена для более простой задачи того же рода.

Предположим, что нам нужно вычислить факториал натурального числа n, но мы уже знаем, как вычислить факториал n минус 1.

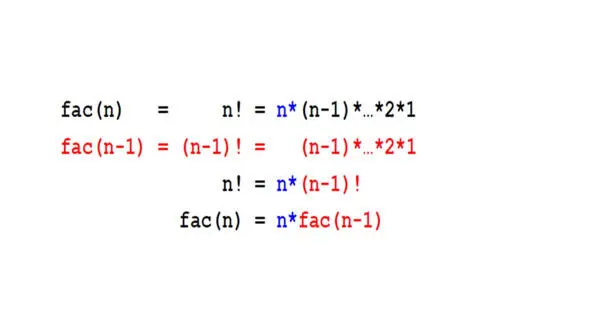
Если бы у нас был факториал n минус 1, мы просто бы умножили это число на n, чтобы получить факториал n.

Вторая часть стратегии – выявить случай, когда предыдущее рассуждение не выполняется.

Факториал 0 нельзя свести к более простому случаю, как мы это делали ранее.

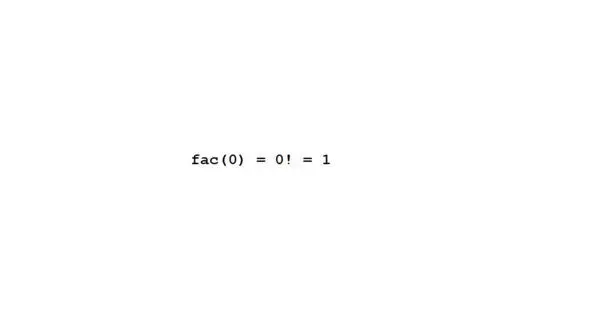
Так что это базовый случай.

Мы просто говорим, что факториал 0 равен 1.

Таким образом, факториал n равен 1, если n равно 0, и факториал n равен n умножить на факториал n минус 1, если n больше 0.

Теперь у нас есть основа для записи рекурсивного метода.

Из математического уравнения легко написать рекурсивный метод.

Там мы видим базовый случай, в котором нет рекурсивного вызова.

Базовый случай получается из пограничного случая.

И мы также видим рекурсивный случай, вытекающий из приведения общего случая к более простому.

Давайте посмотрим на вычислительные возможности калькулятора.

Как правило, калькулятор может делать две вещи: запомнить значения и вычислить новые значения.

Запомнить значения можно с помощью переменных.

И затем мы можем вычислять новые значения с помощью методов.

Например, мы можем сложить два значения, вычесть или умножить.

Таким образом, у нас есть методы, соответствующие арифметике, а также методы, чтобы получить или установить переменную x.

Когда мы пишем программу для моделирования этого калькулятора, и мы определяем для него переменные и методы, мы поместим, с одной стороны, все переменные вместе, а с другой стороны – все методы вместе.

Значения всех переменных в конкретный момент времени будут составлять состояние калькулятора.

И набор методов будет определять поведение калькулятора.

Наша модель будет меняться от одного состояния в другое со временем.

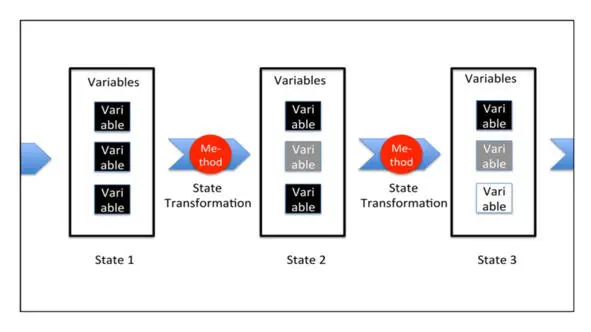
При этом состояние будет определяться значениями переменных.

А методы будут отвечать за изменение состояния.

На самом деле, определение переменных и методов – это общий способ моделирования объектов.

Эти объекты могут соответствовать физическим объектам, например, калькулятору.

Или эти объекты могут быть концептуальными, когда ваш код должен моделировать что-то новое.