Владимир Пахомов - Тайна Календаря. Послание Нерождённым

Здесь нижняя строка таблицы 4 помечена жёлтым цветом.

Теперь я переверну вертикально эту таблицу. Это необходимо только из-за особенностей программы построения изображений и для получения необходимой ориентации изображений.

Итак, я получил перевёрнутую таблицу 5.

Таблица 5

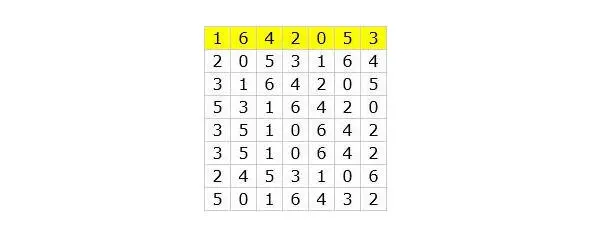
Теперь я беру первую (верхнюю) строку таблицы (она помечена жёлтым цветом). В этой строке, планеты расположены в циклическом порядке Халдейского ряда (см. главу «Звезда Магов»).

1, 6, 4, 2, 0, 5, 3

Используя обход планет по звезде магов, я получаю последовательность:

0, 1, 2, 3, 4, 5, 6

Переставим числа в выбранной строке для получения последовательности – 0, 1, 2, 3, 4, 5, 6. Это принятый порядок дней недели. Для этого необходимо переставить столбцы таблицы( целиком).

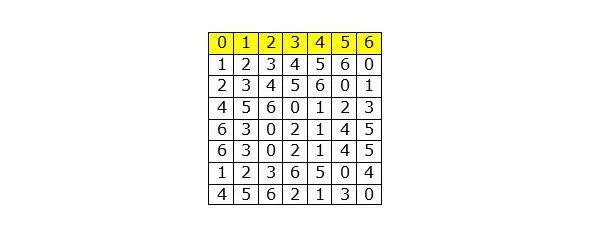
Таблица 6

Это всё, что необходимо сделать. Данные для первого изображения готовы!

Я буду использовать такую перестановку столбцов для получения всех изображений закодированных в матрице Послания. Как видите, здесь данные матрицы Послания не меняются, меняется только порядок её столбцов. Я не добавляю никаких новых чисел, просто переставляю столбцы целикомпо звезде магов.

Всего существует 360 различных вариантов перестановки 7-ми столбцов по первой строке таблицы (см. главу «Круговые перестановки»). Можно сказать, по одной перестановке на каждый день года.

Криптографическая проверка календаря: криптографический механизм проверки встроен в упорядочение столбцов матрицы Послания. При их расположении, дающем обычную последовательность дней недели в какой-либо её строке, матрица Послания даёт данные для получения изображения.

Если столбцы матрицы Послания упорядочить тем же самым методом по второй строке, мы получим второе изображение и так далее.

Восемь строк матрицы Послания дают восемь изображений!

Я подробно объясню создание только первого изображения. Все другие изображения будут получены таким же методом.

«Тополог, это тот, кто не видит различия

между пончиком и кофейной чашкой.»

– Джон Келли

Из математического словаря

Тор (от лат. torus – валик, выпуклость, узел) – тело, образуемое вращением круга вокруг прямой, лежащей в плоскости этого круга, но не пересекающей его. Проще говоря это пончик.

Теперь расскажу о следующем приёме для получения больших изображений, закодированных в Календарном Послании. Представьте себе, что вы имеете один маленький лист бумаги, и вы хотите нарисовать изображение, которое больше чем этот лист бумаги? Как это можно сделать?

Изображение может переходить и с верхнего края листа на нижний край также. То есть верхняя и нижняя грани листа должны быть склеены вместе.

Аналогично, если мы хотим увидеть полное изображение, закодированное в маленькой матрице Послания, необходимо сделать 9 копий этой матрицы. В этом случае изображение будет частично дублироваться, но мы сможем увидеть полное изображение.

Давайте посмотрим, какая фигура получится, если склеить вместе противоположные края листа.

Обычный трёхмерный тор (проще говоря ― пончик) можно сделать из прямоугольника, склеивая обе пары его противоположных граней вместе, без их вращения.

* Если вы будете плыть вокруг Земли, вы возвратитесь в начальную точку. Если вы будете плыть вокруг тора, вы возвратитесь в начальную точку тоже. То есть один этот факт не является доказательством шарообразности Земли.

* Американские учёные заявили о существовании синестии – нового типа планетных объектов. Внешним видом такие космические тела напоминают гигантские пончики с горячим ядром внутри. Более того, специалисты полагают, что когда-то и Земля могла иметь такую форму. Я думаю, что все планеты имеют скрытую, для внешнего наблюдателя, форму тора.

* Обычный тор в трёхмерном пространстве имеет форму подобно пончику, но понятие тора чрезвычайно полезно в пространстве большего числа измерений.

Теперь можно сделать тор из 8×7 таблицы Послания (см., например, таблицу 5). Сделав это, мы получим следующую фигуру.

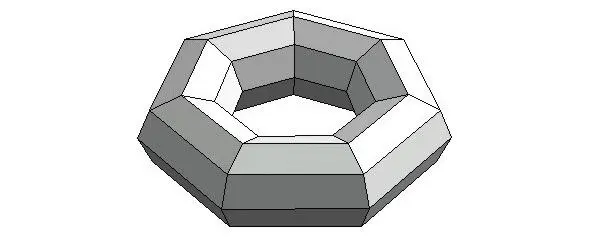
Календарная 8×7 таблица, свёрнутая в тор

Эта фигура напоминает трёхмерную звезду магов. Фигура имеет 56 граней (по числу элементов в календарной матрице). На каждой грани можно написать число (или нарисовать половинку домино) и таким образом поместить всю матрицу Послания на эту фигуру.

Чтобы получить плоскую развёртку изображения сделанного на поверхности тора, необходимо повторить исходную таблицу данных девять раз (см. таблицу 5), как показано ниже.

Используя эти данные можно всегда получить закодированные изображения полностью, с их повторениями.

Почему изображения были сделаны на торе? О чём это говорит нам? Что вы думаете об этом?

Чтобы получить изображения, закодированные в календаре, необходимо знать, какого типа изображениями они являются и каким методом они были закодированы. Есть огромное число различных типов изображений и различных методов, используемых для их кодирования.

Первые научные, графические представления данных связаны с картографией. Картография – это древняя дисциплина, которая известна с доисторического описания территорий охоты и рыболовства.

Самые древние известные нам карты были изображены вавилонянами на глиняных плитках, датируемых приблизительно 2300 г. до н. э. Они не имели ни компьютеров, ни бумаги. Они имели только глину.

Есть много экземпляров хорошо составленных старых карт.

Какого типа изображения закодированы в этой древней матрице Послания? Это не плоские рисунки, это трёхмерныеизображения! Объёмные изображения (барельефы) закодированы в календарном Послании. В этой главе будут получены только плоские проекции этих изображений. Поэтому, то, что вы увидите на экране вашего компьютера, позволит вам получить только идею о реальных трёхмерных объектах, закодированных в календаре.