Владимир Яшин - Информатика: аппаратные средства персонального компьютера

Функция F 4= А называется функцией повторения по логической переменной А.

Функция

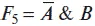
называется функцией запрета по логической переменной В.

Функция F 6= В называется функцией повторения по логической переменной В.

Функция

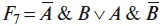
называется функцией исключающее «ИЛИ».

Функция F 8= A v В называется функцией дизъюнкции.

Функция

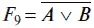
называется функцией Пирса.

Функция

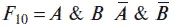
называется функцией эквиваленции.

Функция

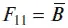
называется функцией отрицания (инверсии) по логической переменной В.

Функция F 12= B ⇒ A называется функцией импликации B ⇒ A.

Функция

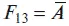
называется функцией отрицания (инверсии) по логической переменной А.

Функция F 14= A ⇒ B называется функцией импликации A ⇒ B .

Функция

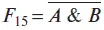
называется функцией Шеффера.

Функция F 16= 1 называется функцией генератора 1.

Среди перечисленных выше логических функций переменных можно выделить несколько логических функций, с помощью которых можно выразить другие логические функции. Операцию замены одной логической функции другой в алгебре логики называют операцией суперпозиции или методом суперпозиции. Например, функцию Шеффера можно выразить при помощи логических функций дизъюнкции и отрицания, используя закон де Моргана:

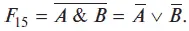
Логические функции, с помощью которых можно выразить другие логические функции методом суперпозиции, называются базовыми логическими функциями. Такой набор базовых логических функций называется функционально полным набором логических функций. На практике наиболее широко в качестве такого набора используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. Если логическая функция представлена с помощью базовых функций, то такая форма представления называется нормальной. В предыдущем примере логическая функция Шеффера, выраженная через базовые функции, представлена в нормальной форме.

При помощи набора базовых функций и соответствующих им технических устройств, реализующих эти логические функции, можно разработать и создать любое логическое устройство или систему.

В настоящее время существует достаточно много программных продуктов, с помощью которых можно реализовать различные логические функции и форму их представления, например в виде таблиц истинности. Логические функции широко используются и в программе MS Excel. Для вызова этих функций необходимо выполнить следующие команды: [Кнопка Пуск– Программы – MS Office ХР – Microsoft Excel] и далее команду: [Вставка – Функция]. В открывшемся окне (рис. 4.4) «Мастер функций – шаг 1 из 2», выберем: «Категория: „Логические“ и далее можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих функций.

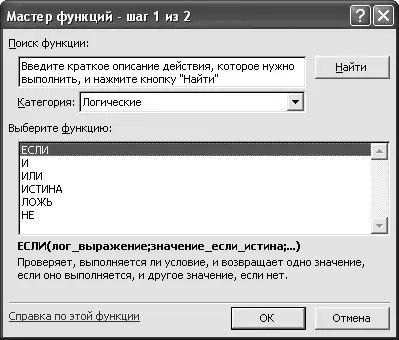
Рис. 4.4. Диалоговое окно «Мастер функций – шаг 1 из 2»

Как видно из рис. 4.4, в состав логических функций программы MS Excel входит функционально полный набор логических функций, состоящий из следующих логических функций: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание). Таким образом, с помощью функционально полного набора логических функций программы MS Excel можно реализовать другие функции. Логическая функция ЕСЛИ (импликация), также входящая в логические функции MS Excel, выполняет логическую проверку и в зависимости от результата проверки выполняет одно из двух возможных действий. В данной программе она имеет следующий формат: = ЕСЛИ (арг1;арг2;арг3), где арг1 – логическое условие; арг2 – возвращаемое значение при условии, что значение аргумента арг1 выполняется (ИСТИНА); арг3 – возвращаемое значение при условии, что значение аргумента арг1 не выполняется (ЛОЖЬ). Например, если в произвольную ячейку листа программы MS Excel ввести выражение « = ЕСЛИ (А1 = 5; „пять“; „не пять“)», то при вводе числа 5 в ячейку А1 и нажатии клавиши «Enter» в ячейке А1 автоматически будет записано слово «пять», при вводе любого другого числа в ячейку А1 в ней запишется слово «не пять». Как уже отмечалось, с помощью логических функций программы MS Excel можно представить другие логические функции и соответствующие им таблицы истинности.

Реализуем с помощью логических функций ЕСЛИ и И модифицированную таблицу истинности логической функции F = А & В (конъюнкции), состоящую из двух строк и трех столбцов, которая позволяет при изменении значений (0 или 1) логических переменных А и В автоматически устанавливать, например, в ячейке Е6 значение функции F = А & В, соответствующее значениям этих логических переменных. Для этого в ячейку Е6 введем следующее выражение: «=ЕСЛИ(И(С6;D6);1;0)», тогда при вводе в ячейки С6 и D6 значений 0 или 1 в ячейке Е6 будет выполняться логическая функция F = А & В. Результат этих действий представлен на рис. 4.5.

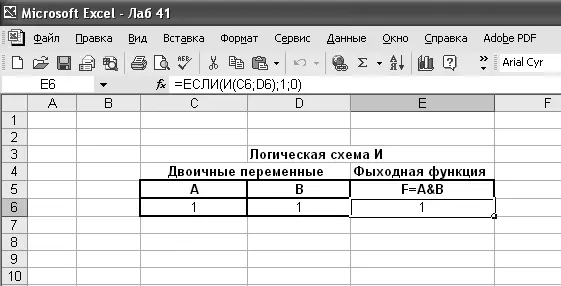
Рис. 4.5. Реализация модифицированной таблицы истинности логической функции F = A & В

Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ÷ 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ÷ 0,4 В) – логическому нулю (ложь).