Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия
- Название:КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия
- Автор:
- Жанр:
- Издательство:БХВ-Петербург
- Год:2010
- Город:СПб
- ISBN:978-5-9775-0602-1
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия краткое содержание
Демонстрируется эффективная компьютерная поддержка курсов черчения, информатики и геометрии на базе свободно распространяемой системы КОМПАС-3D LT. Описываются общие сведения и работа с системой, приводятся основные понятия трехмерного моделирования геометрических объектов. Подробно рассматриваются создание трехмерных моделей деталей и их проекций, нанесение размеров, изображение резьбовых соединений, создание сборок. Показаны возможности применения КОМПАС-3D LT в решении задач графической обработки информации и геометрического трехмерного моделирования. Приводятся примеры решения планиметрических задач и создания 3D-моделей элементарных геометрических тел. В приложениях приводятся эскизные и тестовые задания. DVD содержит дистрибутивы рассматриваемых программ и десятки вариантов практических заданий по всем упоминаемым в книге темам.
Для студентов и преподавателей вузов и колледжей, учащихся и учителей общеобразовательных школ, руководителей курсов повышения квалификации.
КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
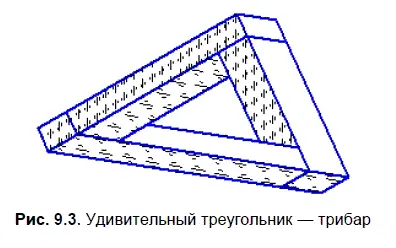
Среди 4-х типов невозможных объектов трибар является первым. За ним следуют «Бесконечная лестница», «Космическая вилка», «Сумасшедший ящик». На примерах покажем, как просто и интересно из трехмерных моделей создавать известные, а возможно, и новые невозможные объекты. В табл. 9.1 показаны этапы создания объекта типа «Трибар».
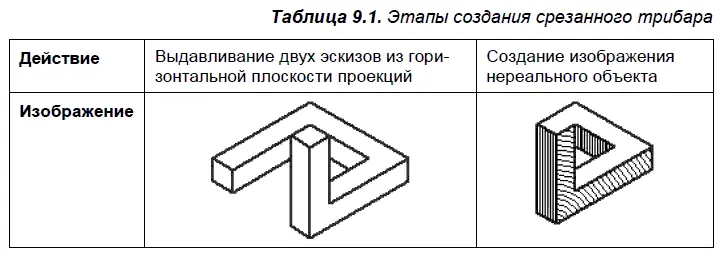
9.2.2. «Бесконечная лестница»
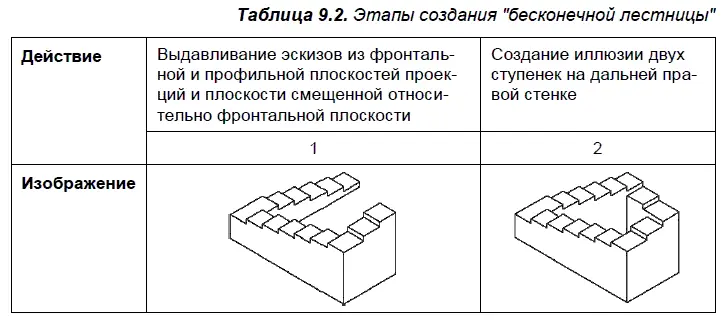
В табл. 9.2–9.5 представлены этапы создания объектов типа «Бесконечная лестница».
«Бесконечная лестница» — одна из самых известных классических невозможностей. В табл. 9.2 предстает лестница, ведущая, казалось бы, вверх или вниз. Но, двигаясь по ней, вам не грозит подняться или опуститься!
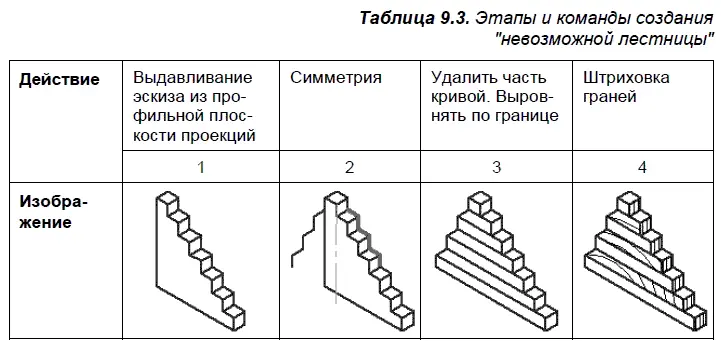
Вверх по «невозможным лестницам». Перед подъемом на лестницу, показанную для действия 1 в табл. 9.3, стоит подумать, как проще этот подъем совершить — по четырем или семи ступенькам? «Похоже, что взобраться наверх проще, если подниматься по левой стороне. Однако, не испробовав, наверняка этого не узнаешь. Законы сохранения энергии могут не сработать в этом странном мире невозможного!» [1]
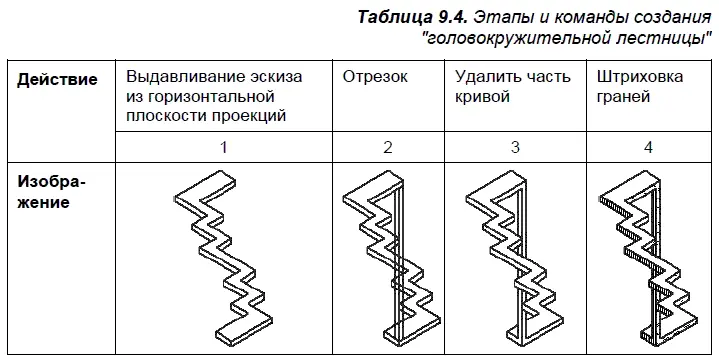
«Головокружительная лестница». Верхняя и нижняя поверхности объекта, показанного для действия 1 в табл. 9.4, казалось бы, плоской дорожки невозможным образом соединяются одним и тем же вертикальным стволом. Невозможность этого ствола обусловлена одновременным существованием его на заднем и переднем планах.
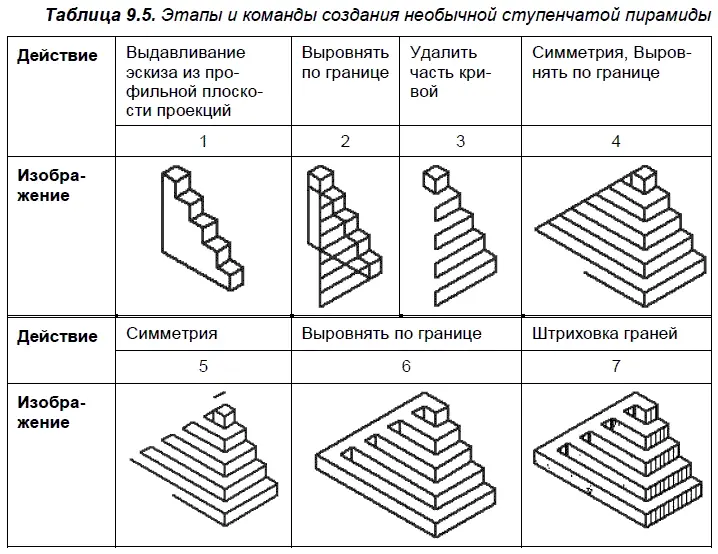
Необычная ступенчатая пирамида. При подъеме на пирамиду, показанную в табл. 9.5, снова надо сделать выбор — можно двигаться по правой стороне и подняться по пяти ступенькам к вершине, а можно просто забраться на плоскость слева, и вы уже наверху! Решайте, что проще?
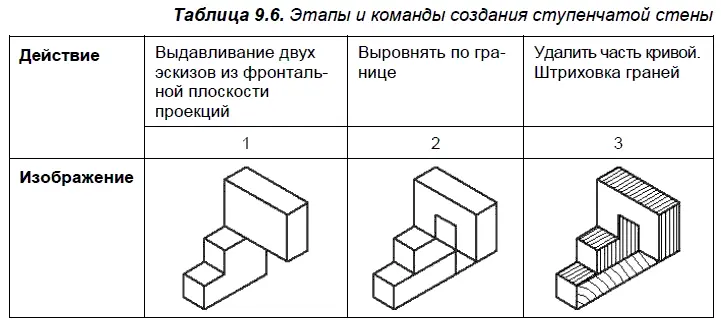
Ступенчатая стена. Передняя поверхность нижней ступеньки объекта из табл. 9.6 «изгибается» вправо, становясь «полом» в основании стены. На таком полу можно и не удержаться на ногах.
9.2.3. «Космическая вилка»
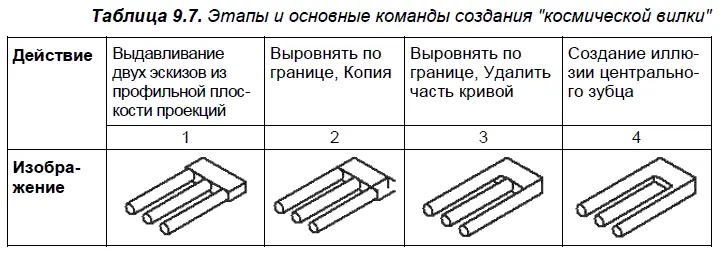
Объекты, представленные в табл. 9.7 и 9.8, относятся к типу «Космическая вилка». Это самый многочисленный класс невозможных объектов.
«Космическая вилка» (табл. 9.7) основана на принципе неправильных соединений, которые возможны в двумерной плоскости, но никак не в трехмерном пространстве. В «Космической вилке» использовано то обстоятельство, что зубец с круглым сечением может быть нарисован с помощью пары параллельных линий. Перекладина же с квадратным сечением — с помощью трех линий. Иллюзия основана на том, что две параллельные линии образуют круглое сечение с одной стороны, прибавляя же к ним третью параллельную линию, мы получим прямоугольное сечение — с другой. Для усиления противоречия все линии строго параллельны в пространстве [1]. Если бы вы смогли сделать поперечное сечение в середине «Космической вилки» — вырезать из нее ломтик, как из батона, — как, по-вашему, он бы выглядел?
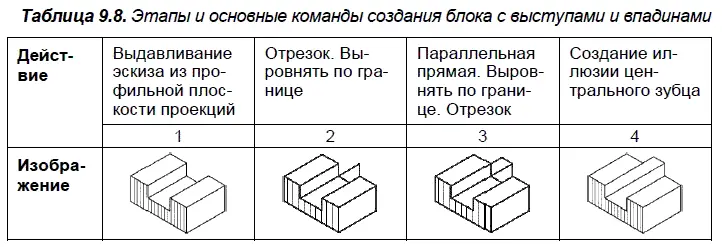
Блок с выступами и впадинами. Невозможность объекта, показанного в табл. 9.8, не требует комментариев. Перечисление в центральных столбцах команд системы КОМПАС показывает инструментальную простоту создания иллюзии неоднозначно изрезанной верхней поверхности объекта средствами этой системы.
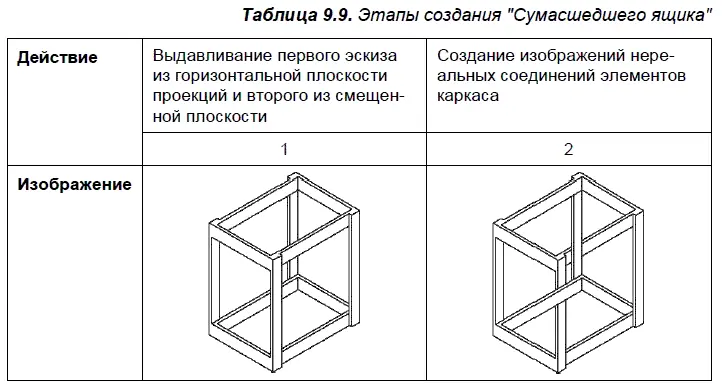
9.2.4. «Сумасшедший ящик»
«Сумасшедший ящик» — это вывернутый наизнанку каркас параллелепипеда. Этот невозможный объект появился в 1966 году в Чикаго, в результате оригинальных экспериментов фотографа доктора Кокрана [1]. «Сумасшедший ящик» основан на неправильных соединениях, допущенных при рисовании. Фигура, показанная в табл. 9.9, воспринимается двояко, при повороте рисунка ящик становится менее сумасшедшим. Переход в нереальный мир осуществляется с помощью двух команд — Удалить | Часть кривой и Выровнять по границе.
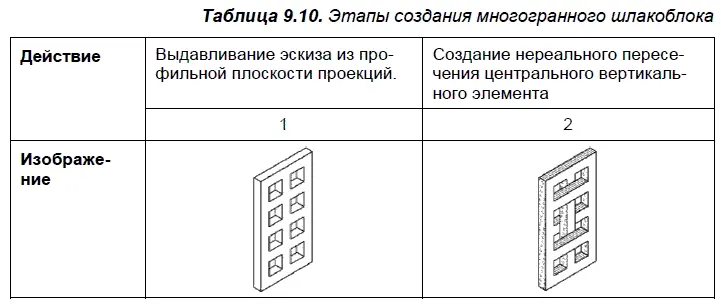
Многогранный шлакоблок. В табл. 9.10 показана одна из вариаций невозможного ящика, являющаяся примером несоответствия плоскостей. Центральный вертикальный элемент беспрепятственно проходит сверху вниз, то ныряя, то возвышаясь над переплетением горизонтальных линий, но при этом не гнется и не ломается.
Построим два объекта, классифицируемых [1] как объекты смешанного типа.
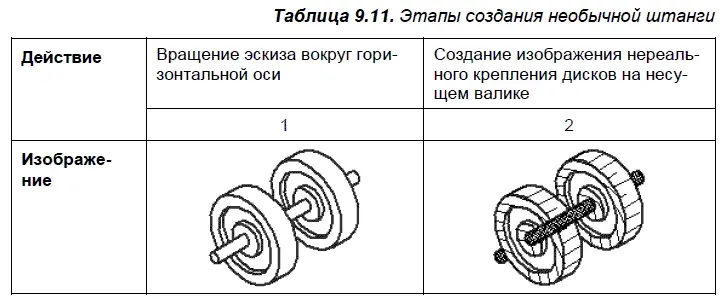
Необычная штанга. Посмотрев на итоговый объект в табл. 9.11, можно задаться вопросом: как прямая штанга проходит вокруг диска, не согнувшись? В мире невозможных объектов — легко!
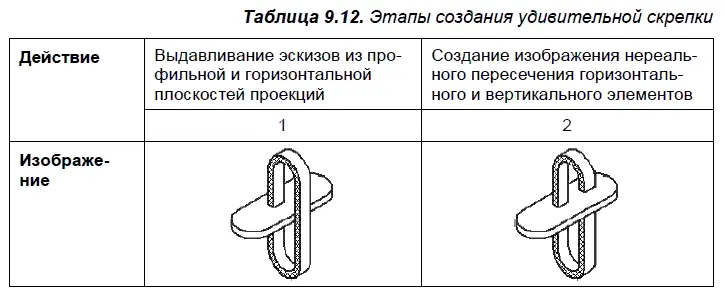
Удивительная скрепка. В табл. 9.12 показано, как просто реальную скрепку превратить в удивительную.
«Ваза-профиль» Рабина (рис. 9.4), варианты которой в большом количестве появлялись в печати, относится к классу двусмысленных объектов. Плоское изображение вазы (рис. 9.4, а) или эскиз для создания 3D-модели (рис. 9.4, б) получаются с помощью команды Кривая Безье.
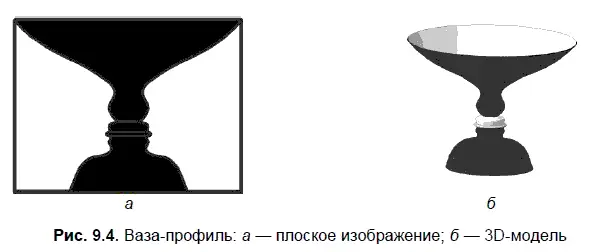
Очевидно, что 3D-модель создается с помощью формообразующей операции Вращение. Грани модели могут быть раскрашены в разные цвета.
9.2.5. Задание для самостоятельной работы
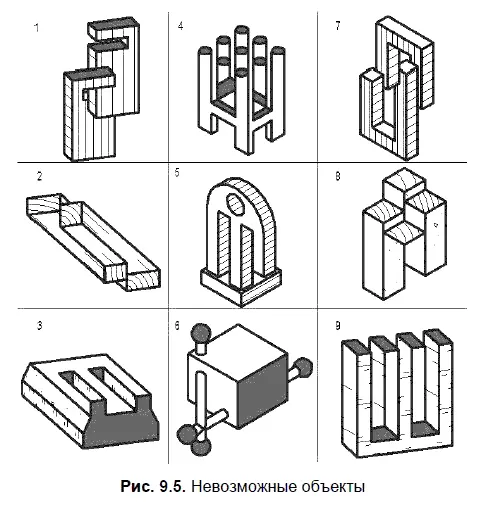
Постройте изображения невозможных объектов (рис. 9.5) в такой последовательности:
Читать дальшеИнтервал:
Закладка:









![Владимир Большаков - Призраки русского замка [litres]](/books/1068592/vladimir-bolshakov-prizraki-russkogo-zamka-litres.webp)
