Турчин Фёдорович - Феномен науки. Кибернетический подход к эволюции

Величину, подлежащую определению, египтяне называли «аха», что переводят как «некоторое количество» или «куча». Вот пример формулировки задачи из египетского папируса: «количество и его четвертая часть дают вместе 15». Это задача «на части» по современной арифметической терминологии, а на алгебраическом языке она соответствует уравнению

x + 1/ 4 x = 15.

Приведем пример более сложной задачи египетских времен.

Квадрат и другой квадрат, сторона которого есть 1/ 2+ 1/ 4стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это.

Решение в современных обозначениях:

x 2+ ( 3/ 4 x ) 2= 100, (1 + 9/ 16) x 2= 100,

5/ 4 x = 10, x = 8, 3/ 4 x = 6,

Описание решения в папирусе:

Возьми квадрат со стороной 1 и возьми 1/ 2+ 1/ 4от 1, т. е. 1/ 2+ 1/ 4в качестве стороны второй площади. Помножь 1/ 2+ 1/ 4на самое себя, это дает 1/ 2+ 1/ 16. Поскольку сторона первой площади взята за 1, а второй за 1/ 2+ 1/ 4, то сложи обе площади вместе; это дает 1 + 1/ 2+ 1/ 16. Возьми корень отсюда: это будет 1 + 1/ 4. Возьми корень из данных 100: это будет 10. Сколько раз входит 1 + 1/ 4в 10? Это входит 8 раз.

Дальше текст не сохранился, но конец очевиден: 8 × 1 = 8 — сторона первого квадрата, 8 × ( 1/ 2+ 1/ 4) = 6 — второго.

Египтяне умели решать только линейные и простейшие квадратные уравнения с одним неизвестным. Вавилоняне продвинулись гораздо дальше. Вот пример задачи из вавилонских текстов.

Площади двух моих квадратов я сложил: 25 25/ 60. Сторона второго квадрата равна 2/ 3стороны первого и еще 5.

Далее следует совершенно правильное ее решение. Эта задача эквивалентна системе уравнений с двумя неизвестными:

x 2+ y 2= 25 25/ 60, y = 2/ 3 x + 5.

Вавилоняне умели решать полное квадратное уравнение

x 2± ax = b ,

кубические уравнения

x 3= a и x 2( x + 1) = a ,

системы уравнений, подобные приведенной выше, а также вида

x 2± y = a , xy = b .

Кроме того, они пользовались формулами

( a + b ) 2= a + 2 ab + b 2и ( a + b )( a - b ) = a 2- b 2,

умели суммировать арифметические прогрессии, знали суммы некоторых числовых рядов и числа, которые впоследствии подучили название пифагоровых (такие целые числа x , y , z , что х 2+ у 2= z 2).

Место древнего Египта и Вавилона в истории математики можно определить следующим образом: в этих культурах впервые появилась формула . Под формулой мы понимаем не только буквенно-цифровое выражение современного алгебраического языка, но вообще всякий языковый объект, являющийся точным (формальным) предписанием, как производить преобразование L 1→ L 2или какие-либо вспомогательные преобразования в рамках языка. Формулы представляют собой важнейшую часть любой развитой теории, хотя, конечно, не исчерпывают ее, ибо в теорию входит еще семантика языковых объектов L i . Утверждение о связи между величинами сторон в прямоугольном треугольнике, содержащееся в теореме Пифагора, — это формула, если даже оно выражено словами, а не буквами. Типовая задача с описанием хода решения («делай так!») и с примечанием, что числа могут быть произвольны (это может быть не высказано, но подразумеваться), — это тоже формула. Именно такие формулы и дошли до нас в египетских папирусах и на вавилонских глиняных табличках.

1 См. замечания И. Н. Веселовского к переводу книги: Ван дёр Варден Б. Пробуждающаяся наука . М.: Физматгиэ, 1959.

2 C небольшими сокращениями.

3 Этот отрывок дошел до нас через Прокла (V в.н.э) — комментатора Евклида.

Ни в египетских, ни в вавилонских текстах мы не находим ничего, что хотя бы отдаленно было похоже на математическое доказательство . Понятие о доказательстве ввели греки, и это является их величайшей заслугой. Какими-то наводящими соображениями при получении новой формулы люди, очевидно, пользовались и раньше, мы даже приводили пример грубо неверной формулы (для площади неправильных четырехугольников у египтян), явно полученной из внешне правдоподобных «общих соображений». Но только греки стали относиться к этим наводящим соображениям с той серьезностью, которой они заслуживают, стали анализировать эти соображения с точки зрения их убедительности и ввели принцип, согласно которому каждое утверждение, касающееся чисел и фигур (формула) , за исключением лишь небольшого числа, должно быть доказано, выведено убедительным, не допускающим сомнений образом из этих «совершенно очевидных» истин. Неудивительно, что именно греки с их демократическим общественным строем создали учение о математическом доказательстве. Споры и доказательство играли важнейшую роль в жизни граждан греческого города-государства ( полиса ). Понятие о доказательстве уже существовало, оно было общественно значимой реальностью. Осталось только перенести его в область математики, что и было сделано, едва греки познакомились с достижениями древних восточных цивилизаций. Сыграло здесь роль, надо полагать, и то положение молодого любознательного ученика, в котором оказались греки по отношению к египтянам и вавилонянам — своим старшим и не всегда согласным друг с другом учителям. В самом деле, вавилоняне определяют площадь круга по формуле 3 r 2, а египтяне по формуле ( 8/ 92 r ) 2. Где же истина? Здесь есть о чем подумать и поспорить.

Творцы египетской и вавилонской математики остались безымянными. Греки сохранили имена своих мудрецов. Первое из них — имя Фалеса Милетского — является также первым именем, вошедшим в историю науки. Фалес жил в VI в. до н. э. в городе Милете на Малоазиатском побережье Эгейского моря. Одна дата из его жизни установлена твердо: в 585 г. до н. э. он предсказал солнечное затмение. Этот факт, кстати, неоспоримо свидетельствует о знакомстве Фалеса с культурой древних цивилизаций, ибо, чтобы установить периодичность затмений, необходим опыт десятков и сотен лет. Так как у Фалеса не было греческих предшественников, он мог заимствовать свои познания по астрономии только у ученых Востока.

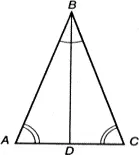
Рис. 10.1. Равнобедренный треугольник

Фалес, как утверждают греки, дал миру первые математические доказательства. В числе доказанных им положений ( теорем ) называют следующие:

Диаметр делит круг на две равные части.

Углы при основании равнобедренного треугольника равны.

Два треугольника, у которых одинаковы стороны и прилежащие к ней углы, равны.

Кроме того, он первый дал построение круга, описанного вокруг прямоугольного треугольника (и в честь этого открытия, как говорят, принес в жертву быка).