Валерий Шилов - Удивительная история информатики и автоматики

Он прославился как создатель и главный идеолог основанной в 1984 году знаменитой компании Thinking Machines, которая разработала самые производительные суперкомпьютеры своего времени Connection Machine. К сожалению, они оказались невостребованными тогдашним рынком, и спустя и лет компания прекратила работы в области суперкомпьютеров.

Однако мало кто помнит о его самой первой, и тоже весьма оригинальной, компьютерной разработке, начало которой относится к 1975 году, когда Хиллис еще учился в Массачусетском технологическом институте. Одним из заданий, полученных студентами его группы, было придумать и собрать из детского конструктора Tin-kertoy какое-либо цифровое устройство. После того, как один из студентов соорудил из деталей конструктора инвертор, который превращает «1» на входе в «о» и наоборот, а второй — логический элемент ИЛИ, стало понятно, что из них можно построить любую другую логическую функцию и, следовательно, любую логическую схему.

Правда, поначалу Хиллис склонялся к мысли построить робота, но затея эта показалась слишком сложной да и требовала немалых затрат, превышавших финансовые возможности студентов. Однако спустя какое-то время директор одного из выставочных центров предложил финансирование, и вскоре Хиллис и его друзья изготовили первый вариант компьютера для игры в «крестики-нолики». Он имел форму куба со стороной 1 метр и был собран из соединенных в логические схемы деталей конструктора. О сделанном ходе компьютер сигнализировал поднимающимся флажком (их было 9, по числу клеток игрового поля). Машина была крайне сложна и требовала тщательной наладки — так что, когда ее в разобранном виде доставили на выставку и вновь собрали, она так и не заработала. Сегодня это уникальное изделие находится в одном из компьютерных музеев США.

В 1979 году из того же выставочного центра поступило предложение — изготовить новый компьютер. Хотя к этому времени Хиллис и его коллеги уже окончили университет и работали не только на разных фирмах, но даже в разных странах, предложение их заинтересовало.

Началась совместная работа — хотя общение в основном шло по телефону.

На этот раз было решено уделить особое внимание надежности — отсюда вытекало требование простоты конструкции. Требовалось решить три основные задачи: как задавать позицию на игровом поле, как ее распознавать и как выбирать следующий ход компьютера. Однако общее число возможных позиций в игре весьма велико, и было необходимо каким-то образом его уменьшить. Понятно, что симметричные позиции можно рассматривать как одну, но ведь надо было научить компьютер такие позиции распознавать. Дерево игры было досконально изучено с помощью специально написанной программы, и было замечено, что многие ходы являются вынужденными: например, если в одном ряду уже стоят два крестика, то, чтобы не проиграть, соперник должен поставить свой нолик именно в этом ряду. Тщательный анализ позволил сократить количество подлежащих рассмотрению значащих позиций до 48.

После этого началась конструкторская работа. Каждую позицию на игровом поле решили представлять осью с набором насаженных на нее колес (назовем ее осью игровых позиций или просто осью позиций). Ось разделена на 9 равных смежных частей, хранящих информацию о состоянии одной из 9 клеток игрового поля. Каждая часть, в свою очередь, содержит три равных отрезка. Отрезок может быть занят колесиком или оставаться незанятым. Если колесики находятся в отрезках 2 и з, это означает, что в соответствующей клетке записан «крестик», если они находятся в отрезках 1 и 2 — «нолик», а в отрезках 1 и з — что клетка пуста (кроме того, отсутствие всех трех колесиков означает, что содержимое клетки не имеет значения). Всего таких осей в машине 48, по количеству значащих позиций. Они закреплены в жесткой установленной вертикально раме.

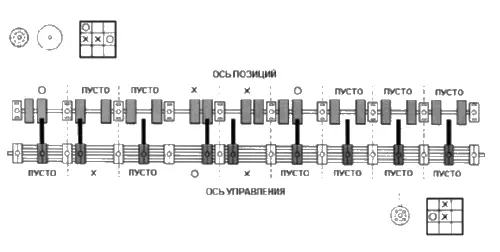
Задача распознавания позиции была решена следующим образом. В конструкцию была введена еще одна ось — ось управления, состоящая из 9 секций равной длины, каждая из которых содержит одно колесико и соответствует одной клетке игрового поля. В зависимости от содержимого клетки колесико может находиться в одном из трех положений. Оператор приводит ось управления в движение, и она начинает перемещаться в вертикальной плоскости вдоль набора осей позиций. Ось управления при этом стремится повернуться так, чтобы выступающие из ее колесиков стержни заняли положение, перпендикулярное плоскости движения. Однако при несовпадении состояний оси позиций и оси управления этого не происходит — хотя бы один из стержней удерживается колесиком на оси позиций, что не позволяет оси управления повернуться.

Если же их состояния совпадают, то ось управления поворачивается, и при этом посредством весьма хитроумного механизма освобождает сигнальный флажок, находящийся напротив соответствующей оси позиций. Флажок поворачивается и закрывает написанную на вертикальной бумажной ленте цифру. Эта цифра и означает, в какую клетку компьютер сделает свой следующий ход.

К сожалению, позднее «игрушечный компьютер» был разобран (кстати, для его изготовления потребовалось 30 комплектов конструктора по 250 деталей в каждом). Сегодня о нем стоит вспомнить не только потому, что это был первый оригинальный проект будущего выдающегося конструктора). «Игрушечный компьютер» заставляет задуматься о том, что же такое компьютер вообще. Сегодня мы привыкли ассоциировать компьютер с электроникой. Но ведь компьютер может быть построен из самых разных элементов — не только механических (как в данном случае), электрических или оптических, но даже гидравлических или пневматических. И даже — из пока непривычных нам биологических.

По прогнозам ученых, в ближайшие 15–20 лет появятся вычислительные машины совершенно нового типа — молекулярные компьютеры, которые будут в миллиарды раз производительнее, чем нынешние электронные компьютеры. Вместо кремниевых транзисторов в них будут использоваться органические и другие молекулы. Правда, не любые, а имеющие несколько (не менее двух) устойчивых состояний. Изменение их состояния под влиянием различных внешних воздействий (например, химических реакций) в некотором смысле эквивалентно переключению из «о» в «1» и обратно. А это значит, что из таких молекул можно создать устройства, моделирующие работу любой логической схемы. Считается, что впервые идея молекулярного компьютера была реализована в 1994 году американским исследователем Леонардом Аделманом. В своих опытах он показал, как можно успешно решать сложные переборные задачи из области теории графов, и в частности, известную «задачу коммивояжера», в которой требуется найти кратчайший маршрут обхода всех вершин графа. Оказалось, что все варианты решения (каждый из которых закодирован одной из нитей ДНК) могут быть получены в лабораторной пробирке посредством ряда биохимических реакций, после чего остается лишь отделить нить ДНК, соответствующую решению.