Александр Леоненков - Самоучитель UML

В контексте языка UML деятельность (activity) представляет собой некоторую совокупность отдельных вычислений, выполняемых автоматом. При этом отдельные элементарные вычисления могут приводить к некоторому результату или действию (action). На диаграмме деятельности отображается логика или последовательность перехода от одной деятельности к другой, при этом внимание фиксируется на результате деятельности. Сам же результат может привести к изменению состояния системы или возвращению некоторого значения.

Примечание 57 Примечание 57 Хотя диаграмма деятельности предназначена для моделирования поведения систем, время в явном виде отсутствует на этой диаграмме. Ситуация здесь во многом аналогична диаграмме состояний.

Состояние действия (action state) является специальным случаем состояния с некоторым входным действием и по крайней мере одним выходящим из состояния переходом. Этот переход неявно предполагает, что входное действие уже завершилось. Состояние действия не может иметь внутренних переходов, поскольку оно является элементарным. Обычное использование состояния действия заключается в моделировании одного шага выполнения алгоритма (процедуры) или потока управления.

Графически состояние действия изображается фигурой, напоминающей прямоугольник, боковые стороны которого заменены выпуклыми дугами (рис. 7.1). Внутри этой фигуры записывается выражение действия (action-expression), которое должно быть уникальным в пределах одной диаграммы деятельности.

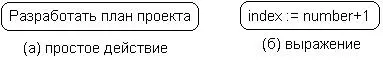
Рис. 7.1.Графическое изображение состояния действия

Действие может быть записано на естественном языке, некотором псевдокоде или языке программирования. Никаких дополнительных или неявных ограничений при записи действий не накладывается. Рекомендуется в качестве имени простого действия использовать глагол с пояснительными словами (рис. 7.1, а). Если же действие может быть представлено в некотором формальном виде, то целесообразно записать его на том языке программирования, на котором предполагается реализовывать конкретный проект (рис. 7.1, б).

Иногда возникает необходимость представить на диаграмме деятельности некоторое сложное действие, которое, в свою очередь, состоит из нескольких более простых действий. В этом случае можно использовать специальное обозначение так называемого состояния под-деятельности (subactivity state). Такое состояние является графом деятельности и обозначается специальной пиктограммой в правом нижнем углу символа состояния действия (рис. 7.2). Эта конструкция может применяться к любому элементу языка UML, который поддерживает «вложенность» своей структуры. При этом пиктограмма может быть дополнительно помечена типом вложенной структуры.

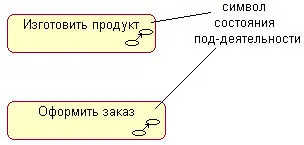
Рис. 7.2.Графическое изображение состояния под-деятельности

Каждая диаграмма деятельности должна иметь единственное начальное и единственное конечное состояния. Они имеют такие же обозначения, как и на диаграмме состояний (см. рис. 6.4). При этом каждая деятельность начинается в начальном состоянии и заканчивается в конечном состоянии. Саму диаграмму деятельности принято располагать таким образом, чтобы действия следовали сверху вниз. В этом случае начальное состояние будет изображаться в верхней части диаграммы, а конечное – в ее нижней части.

Переход как элемент языка UML был рассмотрен в главе 6. При построении диаграммы деятельности используются только нетриггерные переходы, т. е. такие, которые срабатывают сразу после завершения деятельности или выполнения соответствующего действия. Этот переход переводит деятельность в последующее состояние сразу, как только закончится действие в предыдущем состоянии. На диаграмме такой переход изображается сплошной линией со стрелкой.

Если из состояния действия выходит единственный переход, то он может быть никак не помечен. Если же таких переходов несколько, то сработать может только один из них. Именно в этом случае для каждого из таких переходов должно быть явно записано сторожевое условие в прямых скобках (см. главу 6). При этом для всех выходящих из некоторого состояния переходов должно выполняться требование истинности только одного из них. Подобный случай встречается тогда, когда последовательно выполняемая деятельность должна разделиться на альтернативные ветви в зависимости от значения некоторого промежуточного результата. Такая ситуация получила название ветвления, а для ее обозначения применяется специальный символ.

Графически ветвление на диаграмме деятельности обозначается небольшим ромбом, внутри которого нет никакого текста (рис. 7.3). В этот ромб может входить только одна стрелка от того состояния действия, после выполнения которого поток управления должен быть продолжен по одной из взаимно исключающих ветвей. Принято входящую стрелку присоединять к верхней или левой вершине символа ветвления. Выходящих стрелок может быть две или более, но для каждой из них явно указывается соответствующее сторожевое условие в форме булевского выражения.

В качестве примера рассмотрим фрагмент известного алгоритма нахождения корней квадратного уравнения. В общем случае после приведения уравнения второй степени к каноническому виду: а*х*х + Ь*х + с = 0 необходимо вычислить его дискриминант. Причем, в случае отрицательного дискриминанта уравнение не имеет решения на множестве действительных чисел, и дальнейшие вычисления должны быть прекращены. При неотрицательном дискриминанте уравнение имеет решение, корни которого могут быть получены на основе конкретной расчетной формулы. .

Графически фрагмент процедуры вычисления корней квадратного уравнения может быть представлен в виде диаграммы деятельности с тремя состояниями действия и ветвлением (рис. 7.3). Каждый из переходов, выходящих из состояния «Вычислить дискриминант», имеет сторожевое условие, определяющее единственную ветвь, по которой может быть продолжен процесс вычисления корней в зависимости от знака дискриминанта. Очевидно, что в случае его отрицательности, мы сразу попадаем в конечное состояние, тем самым завершая выполнение алгоритма в целом.

Примечание 58 Примечание 58 Строго говоря, первое из состояний рассматриваемого алгоритма следует считать состоянием под-деятельности, поскольку приведение квадратного уравнения к каноническому виду может потребовать нескольких элементарных действий (приведение подобных и перенос отдельных членов уравнения из правой его части в левую). Поэтому для данного состояния целесообразно добавить соответствующую пиктограмму (как на рис. 7.2).