Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Объединение.Какие обезьянки принадлежат либо S 1, либо S 2? Ответ: обезьянки в S 3= { , , }. Новое множество — объединение двух предыдущих. Мы записываем это так: S 3= S 1 S 2.

Пересечение.Какие обезьянки принадлежат и S 1, и S 2? Ответ: обезьянки в S 4= { }. Новое множество получается путем пересечения двух предыдущих. Мы записываем это так: S 4= S 1 S 2.

Степенные множества.Обратите внимание, что S 3и S 4одновременно являются подмножествами S . Мы также полагаем, что S 5= S и пустое множество S 6= {} являются подмножествами S . Если подсчитать все подмножества S , то вы найдете 2 4= 16 подмножеств. Если же рассматривать их все как объекты, то мы можем собрать их в множество. Множество всех подмножеств S называется его степенным множеством :

P S= { S 1, S 2, S 16}.

В разделе «Полный перебор» главы 3 мы представили задачу «Лучшая сделка».

Лучшая сделка У вас есть список цен на золото по дням за какой-то интервал времени. В этом интервале вы хотите найти такие два дня, чтобы, купив золото, а затем продав его, вы получили бы максимально возможную прибыль.

В разделе «Динамическое программирование» той же главы мы показали алгоритм, который решил эту задачу с временной сложностью O ( n ) и пространственной сложностью O ( n ). Когда в 1984 году Джей Кэдейн обнаружил эту задачу, он нашел способ решить ее с O ( n ) по времени и O (1) по пространству:

function trade_kadane(prices):

····sell_day ← 1

····buy_day ← 1

····best_profit ← 0

····for each s from 2 to prices.length

········if prices[s] < prices[buy_day]

············b ← s

········else

············b ← buy_day

········profit ← prices[s] — prices[b]

········if profit > best_profit

············sell_day ← s

············buy_day ← b

············best_profit ← profit

····return (sell_day, buy_day)

Дело в том, что нам незачем хранить день лучшей покупки для каждого дня на входе. Достаточно сохранить день лучшей покупки относительно дня лучшей продажи, найденной к настоящему моменту.

Рисунок использован с согласия http://xkcd.com.

См., например, http://code.energy/coding-courses.

Адаптация схемы с сайта http://wikipedia.org.

См., например, http://code.energy/coding-courses.

Здесь 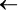означает оператор присваивания: x 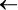1 следует читать как «Присвоить x значение 1».

Любезно предоставлено http://ctp200.com.

Любезно предоставлено http://programmers.life.

В нечеткой логике значения могут быть промежуточными, но в этой книге она рассматриваться не будет.

И, между прочим , они оба фактически истинные.

Названа так в честь Джорджа Буля (1815–1864). Его публикации положили начало математической логике.

Огастес де Морган дружил с Джорджем Булем. Кроме того, он обучал молодую Аду Лавлейс, ставшую первым программистом за век до того, как был создан первый компьютер.

Например, таблица истинности для 30 переменных будет иметь более миллиарда строк .

См. http://code.energy/zebra-puzzle.

True = 1, False = 0. Если вы не знаете, почему 101 — это 5 в двоичной системе счисления, загляните в приложение I.

В 2016 году был создан действующий транзистор с размером 1 нм. Для справки: атом золота имеет размер 0,15 нм.

Комбинаторика и логика относятся к одной из важнейших областей информатики, которая называется дискретной математикой.

По определению 0! = 1. Мы говорим, что ноль элементов, то есть пустое множество, можно упорядочить единственным способом.

В литературе принято обозначение 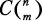( m — нижний индекс, n — верхний), которое читается как «сочетания m из n ». — Примеч. пер.

Профессиональная подсказка: поищите в Интернете по запросу « из 64 по 8 », чтобы узнать результат.

Любезно предоставлено http://xkcd.com.

См. http://wolframalpha.com.

Любезно предоставлено http://xkcd.com.

Чтобы разобраться в алгоритме, выполните его на бумаге с небольшим объемом входящих данных.

(см. раздел «Комбинаторика»).

Читаются такие конструкции следующим образом: «алгоритм сортировки имеет временную сложность o-n-квадрат».

По поводу сложностей большого «О» большинства алгоритмов, которые выполняют типовые задачи, смотрите http://code.energy/bigo.

Было доказано, что неэкспоненциальный алгоритм для любой NP-полной задачи может быть обобщен для всех NP-полных задач. Поскольку мы не знаем, существует ли такой алгоритм, вы также получите миллион долларов, если докажете, что NP-полная задача не может быть решена с использованием неэкспоненциальных алгоритмов.

Объем входных данных (так называемый размер входа) — это число элементов в обоих входных списках, взятых вместе. Цикл while выполняет три операции для каждого из этих элементов, следовательно, T( n ) = 3 n .

Если вам нужно больше узнать о множествах, см. приложение III.

Палиндромы — это слова и фразы, которые читаются одинаково в обе стороны, например «Ада», «топот», «ротатор».

Любезно предоставлено http://geek-and-poke.com.

В интервале n дней имеется n (n + 1)/2 пар дней (см. раздел «Комбинаторика» главы 1).

Подробнее о степенных множествах см. в приложении III.

Задача о рюкзаке является частью класса NP-полных задач, который мы обсудили в разделе 2.3. Вне зависимости от стратегии ее решают только экспоненциальные алгоритмы.