Энтони Уильямс - Параллельное программирование на С++ в действии. Практика разработки многопоточных программ

Использование описанных выше средств синхронизации в качестве строительных блоков позволяет сосредоточиться на самих нуждающихся в синхронизации операциях, а не на механизмах реализации. В частности, код можно упростить, применяя более функциональный (в смысле функционального программирования ) подход к программированию параллелизма. Вместо того чтобы напрямую разделять данные между потоками, мы можем снабдить каждый поток необходимыми ему данными, а результаты вычисления предоставить другим потокам, которые в них заинтересованы, с помощью будущих результатов.

Термином функциональное программирование (ФП) называют такой стиль программирования, при котором результат функции зависит только от ее параметров, но не от внешнего состояния. Это напрямую соотносится с понятием функции в математике и означает, что если два раза вызвать функцию с одними и теми же параметрами, то получатся одинаковые результаты. Таким свойством обладают многие математические функции в стандартной библиотеке С++, например sin, cosи sqrt, а также простые операции над примитивными типами, например 3+3, 6*9или 1.3/4.7. Чистая функция не модифицирует никакое внешнее состояние, она воздействует только на возвращаемое значение.

При таком подходе становится проще рассуждать о функциях, особенно в присутствии параллелизма, поскольку многие связанные с разделяемой памятью проблемы, обсуждавшиеся в главе 3, просто не возникают. Если разделяемые данные не модифицируются, то не может быть никакой гонки и, стало быть, не нужно защищать данные с помощью мьютексов. Это упрощение настолько существенно, что в программировании параллельных систем все более популярны становятся такие языки, как Haskell [9] http://www.haskell.org/. , где все функции чистые по умолчанию . В таком окружении нечистые функции, которые все же модифицируют разделяемые данные, отчетливо выделяются, поэтому становится проще рассуждать о том, как они укладываются в общую структуру приложения.

Но достоинства функционального программирования проявляются не только в языках, где эта парадигма применяется по умолчанию. С++ — мультипарадигменный язык, и на нем, безусловно, можно писать программы в стиле ФП. С появлением в С++11 лямбда-функций (см. приложение А, раздел А.6), включением шаблона std::bindиз Boost и TR1 и добавлением автоматического выведения типа переменных (см. приложение А, раздел А.7) это стало даже проще, чем в С++98. Будущие результаты — это последний элемент из тех, что позволяют реализовать на С++ параллелизм в стиле ФП; благодаря передаче будущих результатов результат одного вычисления можно сделать зависящим от результата другого без явного доступа к разделяемым данным .

Чтобы продемонстрировать использование будущих результатов при написании параллельных программ в духе ФП, рассмотрим простую реализацию алгоритма быстрой сортировки Quicksort. Основная идея алгоритма проста: имея список значений, выбрать некий опорный элемент и разбить список на две части — в одну войдут элементы, меньшие опорного, в другую — большие или равные опорному. Отсортированный список получается путем сортировки обоих частей и объединения трех списков: отсортированного множества элементов, меньших опорного элемента, самого опорного элемента и отсортированного множества элементов, больших или равных опорному элементу. На рис. 4.2 показано, как этот алгоритм сортирует список из 10 целых чисел. В листинге ниже приведена последовательная реализация алгоритма в духе ФП; в ней список принимается и возвращается по значению, а не сортируется по месту в std::sort().

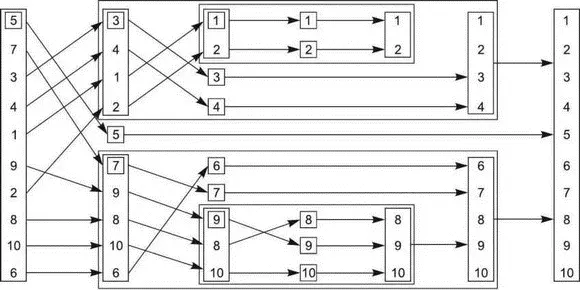
Рис. 4.2.Рекурсивная сортировка в духе ФП

Листинг 4.12. Последовательная реализация Quicksort в духе ФП

template

std::list sequential_quick_sort(std::list input) {

if (input.empty()) {

return input;

}

std::list result;

result.splice(result.begin(), input, input.begin());← (1)

T const& pivot = *result.begin(); ← (2)

auto divide_point = std::partition(input.begin(), input.end(),

[&](T const& t) { return t < pivot; });← (3)

std::list lower_part;

lower_part.splice(

lower_part.end(), input, input.begin(), divide_point); ← (4)

auto new_lower(

sequential_quick_sort(std::move(lower_part))); ← (5)

auto new_higher(

sequential_quick_sort(std::move(input))); ← (6)

result.splice(result.end(), new_higher); ← (7)

result.splice(result.begin(), new_lower); ← (8)

return result;

}

Хотя интерфейс выдержан в духе ФП, прямое применение ФП привело бы к неоправданно большому числу операций копирования, поэтому внутри мы используем «обычный» императивный стиль. В качестве опорного мы выбираем первый элемент и отрезаем его от списка с помощью функции splice() (1). Потенциально это может привести к неоптимальной сортировке (в терминах количества операций сравнения и обмена), но любой другой подход при работе с std::listможет существенно увеличить время за счет обхода списка. Мы знаем, что этот элемент должен войти в результат, поэтому можем сразу поместить его в список, где результат будет храниться. Далее мы хотим использовать этот элемент для сравнения, поэтому берем ссылку на него, чтобы избежать копирования (2). Теперь можно с помощью алгоритма std::partitionразбить последовательность на две части: меньшие опорного элемента и не меньшие опорного элемента (3). Критерий разбиения проще всего задать с помощью лямбда-функции; мы запоминаем ссылку в замыкании, чтобы не копировать значение pivot(подробнее о лямбда-функциях см. в разделе А.5 приложения А).

Алгоритм std::partition()переупорядочивает список на месте и возвращает итератор, указывающий на первый элемент, который не меньше опорного значения. Полный тип итератора довольно длинный, поэтому мы используем спецификатор типа auto, чтобы компилятор вывел его самостоятельно (см. приложение А, раздел А.7).

Раз уж мы выбрали интерфейс в духе ФП, то для рекурсивной сортировки обеих «половин» нужно создать два списка. Для этого мы снова используем функцию splice(), чтобы переместить значения из списка inputдо divide_pointвключительно в новый список lower_part (4). После этого inputбудет со держать только оставшиеся значения. Далее оба списка можно отсортировать путем рекурсивных вызовов (5), (6). Применяя std::move()для передачи списков, мы избегаем копирования — результат в любом случае неявно перемещается. Наконец, мы еще раз вызываем splice(), чтобы собрать result в правильном порядке. Значения из списка new_higherпопадают в конец списка (7), после опорного элемента, а значения из списка new_lower— в начало списка, до опорного элемента (8).