Виталий Ткаченко - Обратные вызовы в C++

Рис. 16. Шкалы оценки реализуемости требований

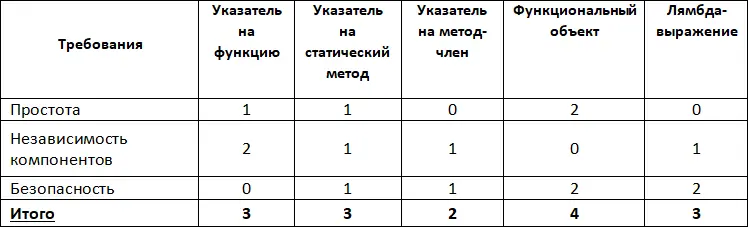
Итак, строим матрицу соответствия, в ячейках выставляем числовые оценки, суммируем оценки по столбцам. Реализация, набравшая наибольшее количество баллов, является оптимальной.

Пример интегральных оценок по трем критериям с использованием трехбалльной шкалы приведен в Табл. 8. Здесь наибольшее количество балов набирает реализация с использованием функционального объекта, которая для конкретного случая является оптимальной.

Табл. 8. Интегральные оценки по трехбалльной шкале

Зачастую оказывается, что некоторые требования являются более важными, чем остальные. Например, быстродействие важно, но в то же время гибкость еще важнее; в свою очередь, безопасность является приоритетным фактором. Чтобы учесть такие ситуации, вводятся коэффициенты важности.

Каждому требованию присваивается коэффициент, который отражает, насколько данное требование является важным для обеспечения качества функционирования системы в конкретном случае. При расчете числовых оценок каждое значение в ячейке таблицы умножается на этот коэффициент; таким образом вносятся поправки в итоговые значения. Целесообразно предварительно ранжировать требования по важности: наименее важному присвоить коэффициент 1, и для каждого требования, более важного, чем предыдущее, увеличивать значение на единицу.

Введем коэффициенты важности для предыдущего примера. Ранжируем требования: считаем, что наименее важным для нас является простота, наиболее важным – безопасность. Результаты приведены в Табл. 9.

Табл. 9. Ранжирование требований

Пересчитаем показатели с учетом коэффициентов важности. Для коэффициентов важности вводим отдельный столбец, где проставляем соответствующие значения. В ячейках в скобках отображаются значения оценки без учета коэффициента, без скобок отображаются новые значения с учетом поправок (Табл. 10).

Табл. 10. Интегральные оценки с учетом коэффициентов важности.

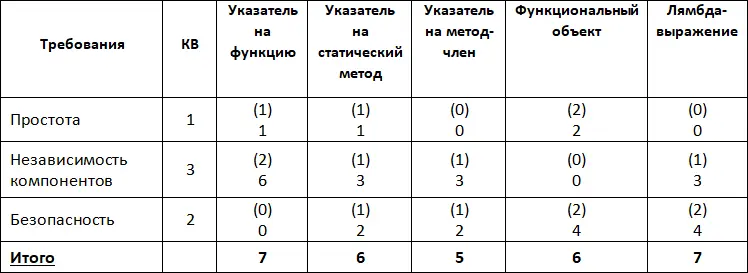
Как видим, после введения коэффициентов важности результаты изменились: теперь максимальное количество балов набирают две реализации – указатель на функцию и лямбда-выражение.

Как мы видели в предыдущем примере, может оказаться, что по результатам расчетов несколько реализаций имеют одинаковое количество балов. В этом случае целесообразно заглянуть в будущее.

Из списка требований выбираем те, которые не актуальны сейчас, но которые, возможно, станут актуальны в последствии. Сводим эти требования в таблицу, аналогично предыдущему примеру, но для числовых значений используем инверсную шкалу: если реализация полностью поддерживает соответствующее требование, выставляем 0, если не поддерживает, то выставляем минимальное отрицательное значение 14 14 Минимальное отрицательное, по модулю оно будет максимальным. . Так, например, если используется трехбалльная шкала, то 0 превращается в -2, 1 превращается в -1, а 2 превращается в 0. Инверсная шкала показывает, насколько сильно новые требования ухудшают текущую интегральную оценку: чем меньше значение 15 15 Мы говорим «меньше», поскольку числа здесь отрицательные. По модулю это значение будет «больше». , тем в большей степени уменьшается текущая оценка.

Далее, полученные оценки суммируются, получившаяся отрицательная интегральная оценка для каждого столбца суммируется с соответствующей текущей оценкой, внося, таким образом, поправки. Из получившихся итоговых значений выбирается реализация, у которой количество балов после коррекции получается наибольшим.

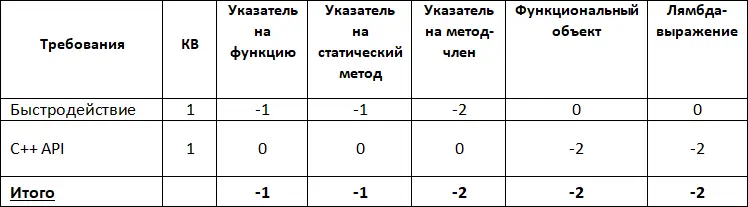
Вернемся к примеру из предыдущего параграфа. Представим, что мы поразмыслили и решили, что в будущем для нас может стать актуальным быстродействие и необходимость реализации C++ API. Сводим эти критерии в таблицу с инверсной шкалой, считаем, что важность этих критериев одинакова. Подсчитываем сумму (Табл. 11).

Табл. 11. Интегральные оценки с инверсной шкалой

Получившиеся результаты суммируем с результатами, полученными с использованием обычной шкалы (Табл. 12).

Табл. 12. Поправки с учетом инверсной шкалы

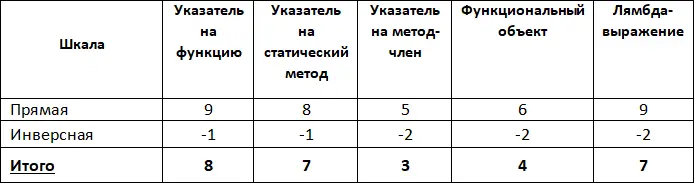
Итак, после внесенных поправок для прогнозных показателей максимальное количество балов набирает указатель на функцию, который рекомендуется к применению.

Может оказаться, что даже после учета прогнозных показателей остаются реализации с одинаковым количеством баллов. В этом случае выбор остается на усмотрение разработчика. Он может, к примеру, взять критерий, который лично для него является более предпочтительным (например, простота), и выбрать реализацию по этому критерию. Или просто выбрать, что называется, первую попавшуюся.

Сравнительный анализ реализаций обратных вызовов необходим для выбора наилучшей в конкретной ситуации. Методика анализа включает в себя выбор объектов, определение критериев сравнения, построение матрицы соответствия, выбор оптимального решения.

Качественный анализ используется, если необходимо выбрать реализацию, оптимальную по какому-нибудь единственному критерию. Если у нас имеется несколько критериев, то необходим количественный анализ, в качестве которого применяется метод интегральных оценок.

Рассмотренные методики подходят не только для исследования обратных вызовов, их можно применять в любых других случаях, когда необходим выбор оптимального архитектурного решения из множества возможных.

Шаблоны в C++ являются инструментом, реализующим параметрический полиморфизм, что означает возможность построения единого (обобщенного) кода для различных типов данных 16 16 В противоположность полиморфизму подтипов, который подразумевает исполнение потенциально разного кода для каждого типа или подтипа. В C++ полиморфизм подтипов реализуется с помощью наследования и виртуальных функций. Термины «параметрический полиморфизм» и «полиморфизм подтипов» больше характерны для академической литературы, в C++ обычно используются их эквиваленты «статический полиморфизм» и «динамический полиморфизм». С точки зрения теории, такая терминология не совсем корректна, потому что она скорее отражает не сущность полиморфизма, а способ его реализации в конкретном языке программирования. Тем не менее, в C++ эти термины прижились. . В таком коде не задаются конкретные типы, а вводятся параметры, в которые затем подставляется нужный тип данных. Чтобы код работал корректно, типы должны удовлетворять некоторым соглашениям, или, другими словами, поддерживать определенный интерфейс.