У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

Рассмотрим следующую базу данных, содержащую сведения о населении и площади некоторых стран в 1976 г. Для представления связи между страной и ее населением будет использоваться предикат нас.В наши дни население обычно характеризуется довольно большими числами. Не все версии Пролога позволяют работать с такими числами. Поэтому будем исчислять население в миллионах: нас(Х, Y)означает, что население страны Xсоставляет примерно « Yмиллионов» людей. Предикат площадьбудет обозначать связь между страной и ее площадью (в миллионах квадратных километров):

нас(сша,203).

нас(индия, 548).

нас(китай,800).

нас(бразилия,108).

площадь(сша,8).

площадь(индия,3).

площадь(китай,9).

площадь(бразилия,8).

Теперь для того, чтобы найти среднюю плотность населения некоторой страны, мы должны использовать правило, гласящее, что значение плотности получается делением числа, представляющего население, на число, представляющее площадь.

Введем предикат плотность(Х,Y), где X – это страна, a Y – плотность населения в данной стране, и запишем соответствующее правило на Прологе:

плотность(X,Y):-нас(Х,Р), площадь(Х,А), Y is Р/А.

Данное правило читается следующим образом:

Плотность населения страны X представляется числом Y, если:

Население X - это Р, и Площадь X - это A, и Y вычисляется делением Р на A.

В правиле используется оператор деления '/' введенный в предыдущем разделе. Операция деления выполняется на самом деле как целочисленное деление, сохраняющее только целую часть результата.

Новым здесь является инфиксный оператор 'is'. Его правый аргумент – терм, интерпретируемый как арифметическое выражение. Для того чтобы выполнить 'is', Пролог сначала вычисляет его правый аргумент в соответствии с правилами арифметики. Результат вычислений проверяется на соответствие с левыми аргументами, чтобы определить, доказуемо ли целевое утверждение. В вышеприведенном примере переменная Yдо исполнения isне конкретизирована, и она остается в таком состоянии до вычисления выражения. Когда выражение вычислено, Yпринимает значение, равное полученной величине. Это означает, что должны быть известны значения всех переменных, находящихся справа от is.

Предикат isнужно использовать каждый раз, когда требуется вычислить арифметическое выражение. Напомним, что конструкции вида Р/Аявляются такими же обычными структурами Пролога, как и автор(эмили,бронте).Но если некоторая структура интерпретируется как арифметическое выражение, то к ней применяется специальная операция, заключающаяся в фактическом выполнении арифметических действий над двоичными представлениями элементов структуры и получении соответствующего результата. Эта операция называется вычислением арифметического выражения. Не любую структуру можно вычислить как арифметическое выражение. Например, очевидно, что нельзя вычислить структуру автор,поскольку функтор авторне определен как арифметическая операция.

Вернемся к примеру со средней плотностью населения. Нетрудно видеть, что типичные вопросы и ответы на них выглядят следующим образом:

?- плотность(китай,X).

X=89

?= плотность(турция,X).

нет

Х=89в первом вопросе представляет собой ответ Пролог-системы, означающий 89 человек на квадратный километр. Второй запрос не выполним, поскольку в базе данных нашего примера невозможно найти сведения о населении Турции.

Набор допустимых арифметических операций зависит от используемой ЭВМ. Однако все Пролог-системы обеспечивают выполнение следующих операций:

X+Y сумма X и Y

X–Y разность X и Y

X*Y произведение X и Y

X/Y частное от деления X на Y

X mod Y остаток от деления X на Y

Этот список вместе со списком операторов сравнения, приведенным выше, содержит все, что необходимо для решения простых арифметических задач. Поскольку Пролог в основном ориентирован на нечисловые задачи, арифметические возможности не так важны, как в других языках программирования.

Для ответа на вопрос, поступивший от программиста, Пролог выполняет решение некоторой задачи. Вопрос содержит конъюнкцию целевых утверждений, которые необходимо попытаться доказать, т. е. проверить на согласованность с базой данных. Для доказательства целевых утверждений Пролог использует известные утверждения. Факт может привести к немедленному доказательству (согласованию) целевого утверждения, в то время как правило может только свести данную задачу к конъюнкции предикатов-подцелей. Однако использование некоторого утверждения возможно только, когда оно «подходит» к рассматриваемому целевому утверждению, т. е. соответствует ему (сопоставимо с ним). Если целевое утверждение не доказано, возбуждается процесс возврата. Процесс возврата заключается в пересмотре проделанной работы и попытках передоказать (вновь согласовать) целевые утверждения путем поиска альтернативных путей доказательства. Более того, если программист неудовлетворен ответом на свой вопрос, он может сам инициировать процесс возврата, нажав на клавиатуре клавишу ';', после того как Пролог информирует его о найденном решении. В данном разделе будут представлены диаграммы, показывающие, как Пролог пытается доказать и передоказать целевые утверждения.

Пролог пытается согласовать с базой данных входящие в конъюнкцию целевые утверждения в том порядке, в каком они написаны (слева направо), где бы они ни появились – в теле правила или в вопросе. Это означает, что Пролог не будет проверять некоторое утверждение, пока не будет доказан его сосед слева. А сосед справа будет рассматриваться только после доказательства данного целевого утверждения. Рассмотрим следующую простую программу о семейных связях:

родители (С,M,F):- мать(С,М), отец(C,F).

мать(джон,анна).

мать(мэри,анна).

отец(мэри,фред). отец(джон,фред).

Давайте рассмотрим последовательность событий, позволяющую дать ответ на вопрос:

?-женщина(мэри), родители(мэри,М,Р), родители(джон,М,Р).

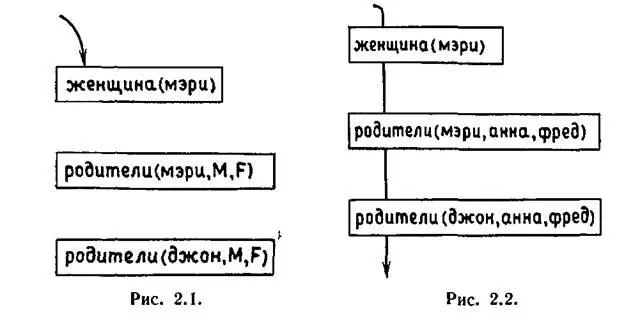
Данный вопрос позволяет определить, является ли мэрисестрой джона. Для того чтобы дать ответ Прологу, необходимо согласовать с базой данных последовательность подцелей, приведенных на рис. 2.1.