Иван Братко - Программирование на языке Пролог для искусственного интеллекта

(1) Начинаем с позиции а .

(2) Переходим к b .

(3) Переходим к d .

(4) Берем максимальную из оценок преемников позиции d , получаем V(d) = 4.

(5) Возвращаемся к b и переходим к e .

(6) Рассматриваем первого преемника позиции e с оценкой 5. В этот момент МАКС (который как раз и должен ходить в позиции e ) обнаруживает, что ему гарантирована в позиции e оценка не меньшая, чем 5, независимо от оценок других (возможно, более предпочтительных) вариантов хода. Этого вполне достаточно для того, чтобы МИН, даже не зная точной оценки позиции e , понял, что для него в позиции b ход в e хуже, чем ход в d .

На основании приведенного выше рассуждения мы можем пренебречь вторым преемником позиции e и приписать e приближенную оценку 5. Приближенный характер этой оценки не окажет никакого влияния на оценку позиции b , а следовательно, и позиции а .

На этой идее основан знаменитый альфа-бета алгоритм , предназначенный для эффективной реализации минимаксного принципа. На рис. 15.4 показан результат работы альфа-бета алгоритма, примененного к нашему дереву рис. 15.2. Из рис. 15.4 видно, что некоторые из рабочих оценок стали приближенными. Однако этих приближенных оценок оказалось достаточно для того, чтобы определить точную оценку корневой позиции. Сложность поиска уменьшилась до пяти обращений к оценочной функции по сравнению с восемью обращениями (в первоначальном дереве поиска рис. 15.2).

Как уже говорилось раньше, ключевая идея альфа-бета отсечения состоит в том, чтобы найти ход не обязательно лучший, но "достаточно хороший" для того, чтобы принять правильное решение. Эту идею можно формализовать, введя два граничных значения, обычно обозначаемых через Альфа и Бета , между которыми должна заключаться рабочая оценка позиции. Смысл этих граничных значений таков: Альфа — это самое маленькое значение оценки, которое к настоящему моменту уже гарантировано для игрока МАКС; Бета — это самое большое значение оценки, на которое МАКС пока еще может надеяться. Разумеется, с точки зрения МИН'а, Бета является самым худшим значением оценки, которое для него уже гарантировано. Таким образом, действительное значение оценки (т.е. то, которое нужно найти) всегда лежит между Альфа и Бета . Если же стало известно, что оценка некоторой позиции лежит вне интервала Альфа-Бета , то этого достаточно для того, чтобы сделать вывод: данная позиция не входит в основной вариант. При этом точное значение оценки такой позиции знать не обязательно, его надо знать только тогда, когда оценка лежит между Альфа и Бета . "Достаточно хорошую" рабочую оценку V( P, Альфа, Бета) позиции P по отношению к Альфа и Бета можно определить формально как любое значение, удовлетворяющее следующим ограничениям:

V( P, Альфа, Бета) ≤ Альфа если V( P) ≤ Альфа

V( P, Альфа, Бета) = V( P) если Альфа < V( P) < Бета

V( P, Альфа, Бета) ≥ Бета если V( P) ≥ Бета

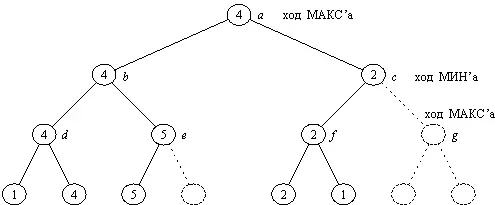
Рис. 15.4. Дерево рис. 15.2 после применения альфа-бета алгоритма. Пунктиром показаны ветви, отсеченные альфа-бета алгоритмом для экономии времени поиска. В результате некоторые из рабочих оценок стали приближенными (вершины c , e , f ; сравните с рис. 15.2). Однако этих приближенных оценок достаточно для вычисления точной оценки корневой вершины и построения основного варианта.

Очевидно, что, умея вычислять "достаточно хорошую" оценку, мы всегда можем вычислить точную оценку корневой позиции P , установив границы интервала следующим образом:

V( P, -бесконечность, +бесконечность) = V( P)

На рис. 15.5 показана реализация альфа-бета алгоритма в виде программы на Прологе. Здесь основное отношение —

альфабета( Поз, Альфа, Бета, ХорПоз, Оц)

где ХорПоз — преемник позиции Позс "достаточно хорошей" оценкой Оц, удовлетворяющей всем указанным выше ограничениям:

Оц = V( Поз, Альфа, Бета)

Процедура

прибл_лучш( СписПоз, Альфа, Бета, ХорПоз, Оц)

находит достаточно хорошую позицию ХорПозв списке позиций СписПоз; Оц — приближенная (по отношению к Альфаи Бета) рабочая оценка позиции ХорПоз.

Интервал между Альфа и Бета может сужаться (но не расширяться!) по мере углубления поиска, происходящего при рекурсивных обращениях к альфа-бета процедуре. Отношение

нов_границы( Альфа, Бета, Поз, Оц, НовАльфа, НовБета)

определяет новый интервал (НовАльфа, НовБета). Он всегда уже, чем старый интервал (Альфа, Бета), или равен ему. Таким образом, чем глубже мы оказываемся в дереве поиска, тем сильнее проявляется тенденция к сжатию интервала Альфа-Бета , и в результате оценивание позиций на более глубоких уровнях происходит в условиях более тесных границ. При более узких интервалах допускается большая степень "приблизительности" при вычислении оценок, а следовательно, происходит больше отсечений ветвей дерева. Возникает интересный вопрос: насколько велика экономия, достигаемая альфа-бета алгоритмом по сравнению с программой минимаксного полного перебора рис. 15.3?

% Альфа-бета алгоритм

альфабета( Поз, Альфа, Бета, ХорПоз, Оц) :-

ходы( Поз, СписПоз), !,

прибл_лучш( СписПоз, Альфа, Бета, ХорПоз, Оц);

стат_оц( Поз, Оц).

прибл_лучш( [Поз | СписПоз], Альфа, Бета, ХорПоз, ХорОц) :-

альфабета( Поз, Альфа, Бета, _, Оц),

дост_хор( СписПоз, Альфа, Бета, Поз, Оц, ХорПоз, ХорОц).

дост_хор( [], _, _, Поз, Оц, Поз, Оц) :- !.

% Больше нет кандидатов

дост_хор( _, Альфа, Бета, Поз, Оц, Поз, Оц) :-

ход_мина( Поз), Оц > Бета, !;

% Переход через верхнюю границу

ход_макса( Поз), Оц < Альфа, !.

% Переход через нижнюю границу

дост_хор( СписПоз, Альфа, Бета, Поз, Оц, ХорПоз, ХорОц) :-

нов_границы( Альфа, Бета, Поз, Оц, НовАльфа, НовБета),

% Уточнить границы

прибл_лучш( СписПоз, НовАльфа, НовБета, Поз1, Оц1),

выбор( Поз, Оц, Поз1, Оц1, ХорПоз, ХорОц).

нов_границы( Альфа, Бета, Поз, Оц, Оц, Бета) :-

ход_мина( Поз), Оц > Альфа, !.

% Увеличение нижней границы

нов_границы( Альфа, Бета, Поз, Оц, Альфа, Оц) :-

ход_макса( Поз), Оц < Бета, !.

% Уменьшение верхней границы

нов_границы( Альфа, Бета, _, _, Альфа, Бета).

выбор( Поз, Оц, Поз1, Оц1, Поз, Оц) :-

ход_мина( Поз), Оц > Оц1, !;

ход_макса( Поз), Оц < Оц1, !.