Иван Братко - Программирование на языке Пролог для искусственного интеллекта

Рис. 4.9. Программа 2 для задачи о восьми ферзях.

Трудность состоит в том, что расположение ферзей определяется только их Y-координатами, а X-координаты в представлении позиции не присутствуют в явном виде. Этой трудности можно избежать путем небольшого обобщения отношения небьет, как это показано на рис. 4.8. Предполагается, что цель

небьет( Ферзь, Остальные)

обеспечивает отсутствие нападении ферзя Ферзьна поля списка Остальныев случае, когда расстояние по X между Ферзьи Остальныеравно 1. Остается рассмотреть более общий случай произвольного расстояния. Для этого мы добавим его в отношение небьетв качестве третьего аргумента:

небьет( Ферзь, Остальные, РасстХ)

Соответственно и цель небьетв отношении безопасныйдолжна быть изменена на

небьет( Ферзь, Остальные, 1)

Теперь отношение небьетможет быть сформулировано в соответствии с двумя случаями, в зависимости от списка Остальные: если он пуст, то бить некого и, естественно, нет нападений; если же он не пуст, то Ферзьне должен бить первого ферзя из списка Остальные(который находится от ферзя Ферзьна расстоянии РасстХвертикалей), а также ферзей из хвоста списка Остальные, находящихся от него на расстоянии РасстХ + 1. Эти соображения приводят к программе, изображенной на рис. 4.9.

Наша третья программа для задачи о восьми ферзях опирается на следующие соображения. Каждый ферзь должен быть размещен на некотором поле, т.е. на некоторой вертикали, некоторой горизонтали, а также на пересечении каких-нибудь двух диагоналей. Для того, чтобы была обеспечена безопасность каждого ферзя, все они должны располагаться в разных вертикалях, разных горизонталях и в разных диагоналях (как идущих сверху вниз, так и идущих снизу вверх). Естественно поэтому рассмотреть более богатую систему представления с четырьмя координатами:

x вертикали

у горизонтали

u диагонали, идущие снизу вверх

v диагонали, идущие сверху вниз

Эти координаты не являются независимыми: при заданных x и у , u и v определяются однозначно (пример на рис. 4.10). Например,

u = x - у

v = x + у

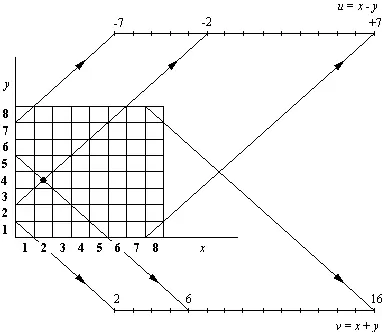
Рис. 4.10. Связь между вертикалями, горизонталями и диагоналями. Помеченное поле имеет следующие координаты: x = 2, у = 4, u = 2 - 4 = -2, v = 2 + 4 = 6.

Области изменения всех четырех координат таковы:

Dx = [1, 2, 3, 4, 5, 6, 7, 8]

Dy = [1, 2, 3, 4, 5, 6, 7, 8]

Du = [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]

Dv = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]

Задачу о восьми ферзях теперь можно сформулировать следующим образом: выбрать восемь четверок (X, Y, U, V), входящих в области изменения (X в Dx, Y в Dy и т.д.), так, чтобы ни один их элемент не выбирался дважды из одной области. Разумеется, выбор X и Y определяет выбор U и V. Решение при такой постановке задачи может быть вкратце таким: при заданных 4-x областях изменения выбрать позицию для первого ферзя, вычеркнуть соответствующие элементы из 4-x областей изменения, а затем использовать оставшиеся элементы этих областей для размещения остальных ферзей. Программа, основанная на таком подходе, показана на рис. 4.11. Позиция на доске снова представляется списком Y-координат. Ключевым отношением в этой программе является отношение

peш( СписY, Dx, Dy, Du, Dv)

которое конкретизирует Y-координаты (в СписY) ферзей, считая, что они размещены в последовательных вертикалях, взятых из Dx. Все Y-координаты и соответствующие координаты U и V берутся из списков Dy, Du и Dv. Главную процедуру решениеможно запустить вопросом

?- решение( S)

Это вызовет запуск решс полными областями изменения координат, что соответствует пространству задачи о восьми ферзях.

решение( СписY) :-

реш( СписY, % Y-координаты ферзей

[1, 2, 3, 4, 5, 6, 7, 8],

% Область изменения Y-координат

[1, 2, 3, 4, 5, 6, 7, 8],

% Область изменения X-координат

[-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7],

% Диагонали, идущие снизу вверх

[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 14, 15, 16] ).

% Диагонали, идущие сверху вниз

реш([], [], Dy, Du, Dv).

реш( [Y | СписY], [X | Dx1], Dy, Du, Dv) :-

удалить( Y, Dy, Dy1), % Выбор Y-координаты

U is X-Y, % Соответствующая диагональ вверх

удалить( U, Du, Du1), % Ее удаление

V is X+Y, % Соответствующая диагональ вниз

удалить( V, Dv, Dv1), % Ее удаление

реш( СписY, Dх1, Dy1, Du1, Dv1).

% Выбор из оставшихся значений

удалить( А, [А | Список], Список).

удалить(A, [В | Список ], [В | Список1 ] ) :-

удалить( А, Список, Список1).

Рис. 4.11. Программа 3 для задачи о восьми ферзях.

Процедура реш универсальна в том смысле, что ее можно использовать для решения задачи об N ферзях (на доске размером N×N). Нужно только правильно задеть области Dx, Dy и т.д.

Удобно автоматизировать получение этих областей. Для этого нам потребуется процедура

генератор( N1, N2, Список)

которая для двух заданных целых чисел N1 и N2 порождает список

Список = [N1, N1 + 1, N1 + 2, ..., N2 - 1, N2]

Вот она:

генератор( N, N, [N]).

генератор( Nl, N2, [Nl | Список]) :-

N1 < N2,

М is N1 + 1,

генератор( М, N2, Список).

Главную процедуру решение нужно соответствующим образом обобщить:

решение( N, S)

где N — это размер доски, а S — решение, представляемое в виде списка Y-координат N ферзей. Вот обобщенное отношение решение:

решение( N, S) :-

генератор( 1, N, Dxy),

Nu1 is 1 - N, Nu2 is N - 1,

генератор( Nu1, Nu2, Du),

Nv2 is N + N,

генератор( 2, Nv2, Dv),

реш( S, Dxy, Dxy, Du, Dv).

Например, решение задачи о 12 ферзях будет получено с помощью:

?- решение( 12, S).

S = [1, 3, 5, 8, 10, 12, 6, 11, 2, 7, 9, 4]

Три решения задачи о восьми ферзях показывают, как к одной и той же задаче можно применять различные подходы. Мы варьировали также и представление данных. В одних случаях это представление было более экономным, в других — более наглядным и, до некоторой степени, избыточным. К недостаткам более экономного представления можно отнести то, что какая-то информация всякий раз, когда она требовалась, должна была перевычисляться.

В некоторых случаях основным шагом к решению было обобщение задачи. Как ни парадоксально, но при рассмотрении более общей задачи решение оказывалось проще сформулировать. Принцип такого обобщения — стандартный прием программирования, и его можно часто применять.