Иван Братко - Программирование на языке Пролог для искусственного интеллекта

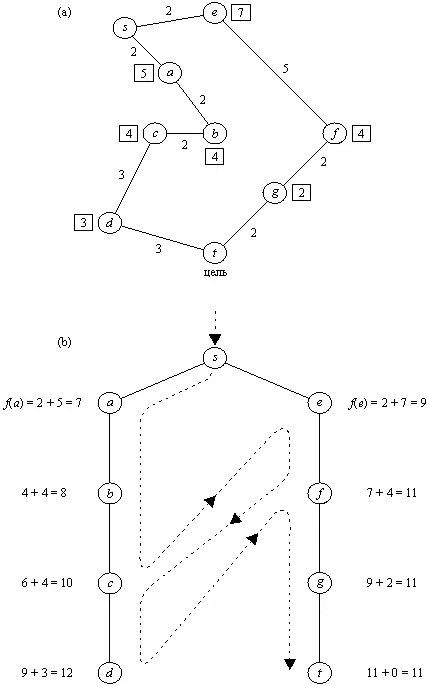
Рис. 12.2. Поиск кратчайшего маршрута из s в t . (а) Карта со связями между городами; связи помечены своими длинами; в квадратиках указаны расстояния по прямой до цели t . (b) Порядок, в котором при поиске с предпочтением происходит обход городов. Эвристические оценки основаны на расстояниях по прямой. Пунктирной линией показано переключение активности между альтернативными путями. Эта линия задает тот порядок, в котором вершины принимаются для продолжения пути, а не тот порядок, в котором они порождаются.

На рис. 12.2 показан пример поведения конкурирующих процессов. Дана карта, задача состоит в том, чтобы найти кратчайший маршрут из стартового города s в целевой город t . В качестве оценки стоимости остатка маршрута из города X до цели мы будем использовать расстояние по прямой расст( X, t) от X до t . Таким образом,

f( X) = g( X) + h( X) = g( X) + расст( X, t)

Мы можем считать, что в данном примере процесс поиска с предпочтением состоит из двух процессов. Каждый процесс прокладывает свой путь — один из двух альтернативных путей: Процесс 1 проходит через а . Процесс 2 — через e . Вначале Процесс 1 более активен, поскольку значения f вдоль выбранного им пути меньше, чем вдоль второго пути. Когда Процесс 1 достигает города с , а Процесс 2 все еще находится в e , ситуация меняется:

f( с) = g( c) + h( c) = 6 + 4 = 10

f( e) = g( e) + h( e) = 2 + 7 = 9

Поскольку f( e) < f( c) , Процесс 2 переходит к f , a Процесс 1 ждет. Однако

f( f) = 7 + 4 = 11

f( c) = 10

f( c) < f( f)

Поэтому Процесс 2 останавливается, а Процессу 1 дается разрешение продолжать движение, но только до d , так как f( d) = 12 > 11 . Происходит активация Процесса 2, после чего он, уже не прерываясь, доходит до цели t .

Мы реализуем этот механизм программно при помощи усовершенствования программы поиска в ширину (рис. 11.13). Множество путей-кандидатов представим деревом. Дерево будет изображаться в программе в виде терма, имеющего одну из двух форм:

(1) л( В, F/G) — дерево, состоящее из одной вершины (листа); В — вершина пространства состояний, G — g ( B) (стоимость уже найденного пути из стартовой вершины в В); F - f ( В) = G + h ( В).

(2) д( В, F/G, Пд) — дерево с непустыми поддеревьями; В — корень дерева, Пд — список поддеревьев; G — g ( B) ; F — уточненное значение f ( В) , т.е. значение f для наиболее перспективного преемника вершины В; список Пдупорядочен в порядке возрастания f -оценок поддеревьев.

Уточнение значения f необходимо для того, чтобы дать программе возможность распознавать наиболее перспективное поддерево (т.е. поддерево, содержащее наиболее перспективную концевую вершину) на любом уровне дерева поиска. Эта модификация f -оценок на самом деле приводит к обобщению, расширяющему область определения функции f . Теперь функция f определена не только на вершинах, но и на деревьях. Для одновершинных деревьев (листов) n остается первоначальное определение

f( n) = g( n) + h( n)

Для дерева T с корнем n , имеющем преемников m 1, m 2, …, получаем

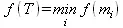
Программа поиска с предпочтением, составленная в соответствии с приведенными выше общими соображениями, показана на рис 12.3. Ниже даются некоторые дополнительные пояснения.

Так же, как и в случае поиска в ширину (рис. 11.13), ключевую роль играет процедура расширить, имеющая на этот раз шесть аргументов:

расширить( Путь, Дер, Предел, Дер1, ЕстьРеш, Решение)

Эта процедура расширяет текущее (под)дерево, пока f -оценка остается равной либо меньшей, чем Предел.

% Поиск с предпочтением

эврпоиск( Старт, Решение) :-

макс_f( Fмакс). % Fмакс > любой f-оценки

расширить( [], л( Старт, 0/0), Fмакс, _, да, Решение).

расширить( П, л( В, _ ), _, _, да, [В | П] ) :-

цель( В).

расширить( П, л( В, F/G), Предел, Дер1, ЕстьРеш, Реш) :-

F <= Предел,

( bagof( B1/C, ( после( В, В1, С), not принадлежит( В1, П)),

Преемники), !,

преемспис( G, Преемники, ДД),

опт_f( ДД, F1),

расширить( П, д( В, F1/G, ДД), Предел, Дер1,

ЕстьРеш, Реш);

ЕстьРеш = никогда). % Нет преемников - тупик

расширить( П, д( В, F/G, [Д | ДД]), Предел, Дер1,

ЕстьРеш, Реш) :-

F <= Предел,

опт_f( ДД, OF), мин( Предел, OF, Предел1),

расширить( [В | П], Д, Предел1, Д1, ЕстьРеш1, Реш),

продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,

ЕстьРеш1, ЕстьРеш, Реш).

расширить( _, д( _, _, []), _, _, никогда, _ ) :- !.

% Тупиковое дерево - нет решений

расширить( _, Дер, Предел, Дер, нет, _ ) :-

f( Дер, F), F > Предел. % Рост остановлен

продолжить( _, _, _, _, да, да, Реш).

продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,

ЕстьРеш1, ЕстьРеш, Реш) :-

( ЕстьРеш1 = нет, встав( Д1, ДД, НДД);

ЕстьРеш1 = никогда, НДД = ДД),

опт_f( НДД, F1),

расширить( П, д( В, F1/G, НДД), Предел, Дер1,

ЕстьРеш, Реш).

преемспис( _, [], []).

преемспис( G0, [В/С | ВВ], ДД) :-

G is G0 + С,

h( В, H), % Эвристика h(B)

F is G + H,

преемспис( G0, ВВ, ДД1),

встав( л( В, F/G), ДД1, ДД).

% Вставление дерева Д в список деревьев ДД с сохранением

% упорядоченности по f-оценкам

встав( Д, ДД, [Д | ДД] ) :-

f( Д, F), опт_f( ДД, F1),

F =< F1, !.

встав( Д, [Д1 | ДД], [Д1 | ДД1] ) ) :-

встав( Д, ДД, ДД1).

% Получение f-оценки

f( л( _, F/_ ), F). % f-оценка листа

f( д( _, F/_, _ ) F). % f-оценка дерева

опт_f( [Д | _ ], F) :- % Наилучшая f-оценка для

f( Д, F). % списка деревьев

опт_f( [], Fмакс) :- % Нет деревьев:

мaкс_f( Fмакс). % плохая f-оценка

мин( X, Y, X) :-

X =< Y, !.

мин( X, Y, Y).

Рис. 12.3. Программа поиска с предпочтением.

Аргументы процедуры расширитьимеют следующий смысл:

Переменные Путь, Дер, и Предел — это "входные" параметры процедуры расширитьв том смысле, что при каждом обращении к расширитьони всегда конкретизированы. Процедура расширитьпорождает результаты трех видов. Какой вид результата получен, можно определить по значению индикатора ЕстьРешследующим образом: