Иван Братко - Программирование на языке Пролог для искусственного интеллекта

(1) ЕстьРеш = да

Решение= решающий путь, найденный при расширении дерева Дерс учетом ограничения Предел.

Дер1= неконкретизировано.

(2) ЕстьРеш = нет

Дер1= дерево Дер, расширенное до тех пор, пока его f -оценка не превзойдет Предел(см. рис. 12.4).

Решение= неконкретизировано.

(3) ЕстьРеш = никогда

Дер1и Решение= неконкретизированы.

В последнем случае Дерявляется "тупиковой" альтернативой, и соответствующий процесс никогда не будет реактивирован для продолжения просмотра этого дерева. Случай этот возникает тогда, когда f -оценка дерева Дерне превосходит ограничения Предел, однако дерево не может "расти" потому, что ни один его лист не имеет преемников, или же любой преемник порождает цикл.

Некоторые предложения процедуры расширитьтребуют пояснений. Предложение, относящееся к наиболее сложному случаю, когда Деримеет поддеревья, т.е.

Дер = д( В, F/G, [Д | ДД ] )

означает следующее. Во-первых, расширению подвергается наиболее перспективное дерево Д. В качестве ограничения этому дереву выдается не Предел, а некоторое, возможно, меньшее значение Предел1, зависящее от f -оценок других конкурирующих поддеревьев ДД. Тем самым гарантируется, что "растущее" дерево — это всегда наиболее перспективное дерево, а переключение активности между поддеревьями происходит в соответствии с их f -оценками. После того, как самый перспективный кандидат расширен, вспомогательная процедура продолжитьрешает, что делать дальше, а это зависит от типа результата, полученного после расширения. Если найдено решение, то оно и выдается, в противном случае процесс расширения деревьев продолжается.

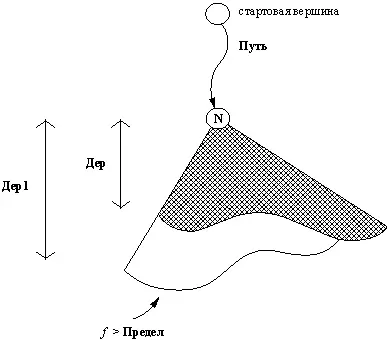
Рис. 12.4. Отношение расширить: расширение дерева Дердо тех пор, пока f -оценка не превзойдет Предел, приводит к дереву Дер1.

Предложение, относящееся к случаю

Дер = л( В, F/G)

порождает всех преемников вершины Ввместе со стоимостями дуг, ведущих в них из В. Процедура преемсписформирует список поддеревьев, соответствующих вершинам-преемникам, а также вычисляет их g- и f- оценки, как показано на рис. 12.5. Затем полученное таким образом дерево подвергается расширению с учетом ограничения Предел. Если преемников нет, то переменной ЕстьРешпридается значение "никогда" и в результате лист Впокидается навсегда.

Другие отношения:

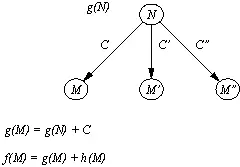
Рис. 12.5. Связь между g- оценкой вершины В и f- и g- оценками ее "детей" в пространстве состояний.

В следующих разделах мы покажем на примерах, как можно применить нашу программу поиска с предпочтением к конкретным задачам. А сейчас сделаем несколько заключительных замечаний общего характера относительно этой программы. Мы реализовали один из вариантов эвристического алгоритма, известного в литературе как А*-алгоритм (ссылки на литературу см. в конце главы). А*-алгоритм привлек внимание многих исследователей. Здесь мы приведем один важный результат, полученный в результате математического анализа А*-алгоритма:

Алгоритм поиска пути называют допустимым , если он всегда отыскивает оптимальное решение (т.е. путь минимальной стоимости) при условии, что такой путь существует. Наша реализация алгоритма поиска, пользуясь механизмом возвратов, выдает все существующие решения, поэтому, в нашем случае, условием допустимости следует считать оптимальность первого из найденных решений. Обозначим через h*(n) стоимость оптимального пути из произвольной вершины n в целевую вершину. Верна следующая теорема о допустимости А*-алгоритма: А*-алгоритм, использующий эвристическую функцию h , является допустимым, если

h ( n ) ≤ h *( n )

для всех вершин n пространства состояний.

Этот результат имеет огромное практическое значение. Даже если нам не известно точное значение h *, нам достаточно найти какую-либо нижнюю грань h * и использовать ее в качестве h в А*-алгоритме — оптимальность решения будет гарантирована.

Существует тривиальная нижняя грань, а именно:

h ( n ) = 0, для всех вершин n пространства состояний.

И при таком значении h допустимость гарантирована. Однако такая оценка не имеет никакой эвристической силы и ничем не помогает поиску. А*-алгоритм при h =0 ведет себя аналогично поиску в ширину. Он, действительно, превращается в поиск в ширину, если, кроме того, положить с ( n , n' )=1 для всех дуг ( n , n' ) пространства состояний. Отсутствие эвристической силы оценки приводит к большой комбинаторной сложности алгоритма. Поэтому хотелось бы иметь такую оценку h , которая была бы нижней гранью h * (чтобы обеспечить допустимость) и, кроме того, была бы как можно ближе к h * (чтобы обеспечить эффективность). В идеальном случае, если бы нам была известна сама точная оценка h *, мы бы ее и использовали: А*-алгоритм, пользующийся h *, находит оптимальное решение сразу, без единого возврата.

12.1. Определите отношения после, цельи h для задачи поиска маршрута рис. 12.2. Посмотрите, как наш алгоритм поиска с предпочтением будет вести себя при решении этой задачи.

Если мы хотим применить программу поиска с предпочтением, показанную на рис. 12.3, к какой-нибудь задаче, мы должны добавить к нашей программе отношения, отражающие специфику этой конкретной задачи. Эти отношения определяют саму задачу ("правила игры"), а также вносят в алгоритм эвристическую информацию о методе ее решения. Эвристическая информация задается в форме эвристической функции.

/* Процедуры, отражающие специфику головоломки

"игра в восемь".

Текущая ситуация представлена списком положений фишек;