Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Код двух последних методов класса синтаксического анализатора регулярных выражений: метода ParseTerm и интерфейсного метода Parse показан в листинге 10.6.

Листинг 10.6. Методы ParseTerm и Parse

procedure TtdRegexParser.rpParseTerm;

begin

rpParseFactor;

if (FPosn^ = '(') or (FPosn^ = '[') or (FPosn^ = '.') or

((FPosn^ <> #0) and not (FPosn^ in Metacharacters)) then

rpParseTerm;

end;

function TtdRegexParser.Parse(var aErrorPos : integer): boolean;

begin

Result := true;

aErrorPos := 0;

{$IFDEF Delphi1}

FPosn := FRegexStrZ;

{$ELSE}

FPosn := PAnsiChar(FRegexStr);

{$ENDIF}

try

rpParseExpr;

if (FPosn^ <> #0) then begin

Result := false;

{$IFDEF Delphi1}

aErrorPos := FPosn - FRegexStrZ + 1;

{$ELSE}

aErrorPos := FPosn - PAnsiChar (FRegexStr) + 1;

{$END1F}

end;

except on E: Exception do

begin

Result := false;

{$IFDEF Delphi1}

aErrorPos := FPosn - FRegexStrZ + 1;

{$ELSE}

aErrorPos := FPosn - PAnsiChar (FRegexStr) + 1;

{$ENDIF}

end;

end;

end;

Итак, мы научились выполнять синтаксический анализ регулярного выражения. Теперь мы может принять строку и вернуть информацию о том, образует ли она допустимое регулярное выражение.

Следующий шаг состоит в создании NFA-автомата для регулярного выражения. Решение этой задачи мы начнем с создания блок-схемы конечного автомата выполнения регулярного выражения. Создание блок-схемы конечного автомата для конкретного регулярного выражения - достаточно простая задача. В общем случае правила языка утверждают, что регулярное выражение состоит из различных подвыражений (которые сами являются регулярными выражениями), скомпонованных или объединенных различными способами. Каждое подвыражение имеет единственное начальное состояние и единственное конечное состояние. И подобно тому, как это делается в конструкторе "Лего", эти простые строительные блоки собираются воедино, образуя все регулярное выражение. Блок-схема, приведенная на рис. 10.6, содержит конструкции, имеющие наибольшее значение.

Первый пример - конечный автомат, выполняющий распознавание отдельного символа алфавита. Второй пример столь же прост: он представляет собой конечный автомат, выполняющий распознавание любого символа алфавита (другими словами, это операция "."). Четвертая конструкция служит иллюстрацией того, как выполняется конкатенация (одного выражения, за которым следует второе). При этом мы просто объединяем начальное состояние второго подвыражения с конечным состоянием первого. Следующей показана конструкция, выполняющая дизъюнкцию. Мы создаем новое начальное состояние и получаем два возможных бесплатных перехода, по одному для каждого из подвыражений. Конечное состояние первого подвыражения объединяется с конечным состоянием второго подвыражения, и это последнее состояние становится конечным состоянием всего выражения. Следующий конечный автомат реализует операцию "?": в данном случае мы создаем новое начальное состояние с двумя ветвями е;

первая выполняет соединение с начальным состоянием подвыражения, а вторая - с его конечным состоянием. Это конечное состояние является конечным состоянием всего выражения. Вероятно, наиболее сложными конструкциями являются конечные автоматы для выполнения операций "+" и "*".

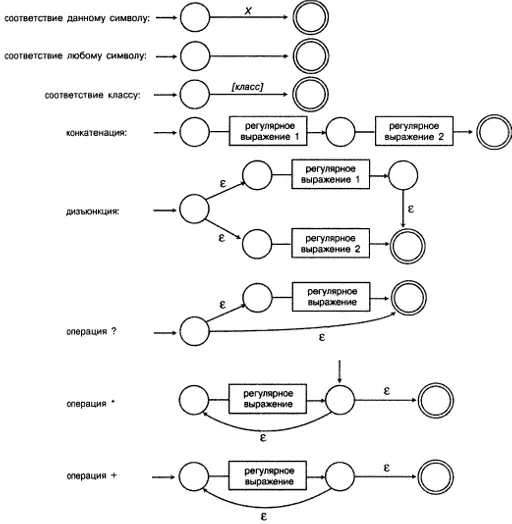
Рисунок 10.6. Конечные NFA-автоматы выполнения операций в регулярных выражениях

Если вы взглянете на рис. 10.6, то наверняка обратите внимание на ряд интересных свойств. В некоторых конструкциях для создания конечных автоматов определены и используются дополнительные состояния, но это делается вполне определенным образом: для каждого состояния существует один или два перехода из него, причем оба являются бесплатными. Это обусловлено веской причиной - в результате кодирование существенно упрощается.

Рассмотрим простой пример: регулярное выражение "(а|b)*bc" (повторенный ноль или более раз символ а или b, за которым следуют символы b и с). Используя описанные конструкции, можно шаг за шагом состроить конечный NFA-автомат для этого регулярного выражения. Последовательность действий показана на рис. 10.7. Обратите внимание, что на каждом шаге мы получаем конечный NFA-автомат с одним начальным и одним конечным состоянием, причем из каждого нового создаваемого состояния возможно не более двух переходов.

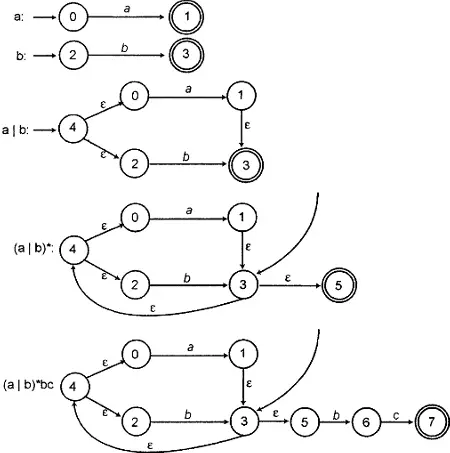
Рисунок 10.7. Пошаговое построение конечного NFA-автомата

Благодаря используемому методу конструирования, можно создать очень простое табличное представление каждого состояния. Каждое состояние будет представлено записью в массиве таких записей (номер состояния является индексом записи в массиве). Запись каждого состояния будет состоять из чего-либо для сравнения и двух номеров состояний для следующего состояния (NextStatel, NextState2). "Что-либо для сравнения" - это шаблон символов, с которым нужно устанавливать соответствие. Им может быть ветвь е, реальный символ, символ операции означающий соответствие с любым символом, класс символов (т.е. набор символов, один из которых должен совпадать с входным символом) или класс символов с отрицанием (входной символ не может быть частью набора, с которым устанавливается соответствие). Будучи построенным, этот массив известен под названием таблицы переходов (trAnsition table). В ней представлены все переходы из одного состояния в другое.

Используя заключительную блок-схему NFA-автомата, показанную на рис. 10.7, можно вручную построить таблицу переходов для регулярного выражения "(a|b)*bc". Результат приведен в таблице 10.1. Мы начинаем с состояния 0 и осуществляем переходы, выполняя сравнение с каждым символом во входной строке, пока не достигнем состояния 7. Реализация алгоритма установки соответствия, использующего подобную таблицу переходов, должна быть очень простой.

Таблица 10.1. Таблица переходов для выражения (a|b)*bc

Теперь, когда мы научились графически представлять NFA-автомат для конкретного регулярного выражения и узнали, что этот конечный NFA-автомат может быть представлен простой таблицей переходов, необходимо объединить оба алгоритма в анализаторе регулярных выражений, чтобы он мог выполнять непосредственную компиляцию таблицы состояний. После этого можно будет приступить к рассмотрению заключительной задачи - сопоставлению строк за счет использования таблицы переходов.

Прежде всего, необходимо выбрать способ представления таблицы состояний. Наиболее очевидный выбор - использование класса TtdRecordList, описанного в главе 2. Этот класс позволяет при необходимости увеличивать размер внутреннего массива. При этом заранее не нужно определять, сколько состояний может существовать для данного регулярного выражения.