Макс Тегмарк - Наша математическая вселенная. В поисках фундаментальной природы реальности

В марте 2008 года Энтони рассказал мне о возможном подходе к решению этой проблемы (я вскоре его изложу), предложенном его гарвардским профессором Дэвидом Лэйзером. Мы провели два замечательных часа в кафе «Белмонт», исписывая салфетки математическими символами, – но все впустую. Мы не смогли заставить работать эту математику. Но я не мог и выкинуть эту идею из головы. Два года спустя я нашел статью, написанную в 1968 году теоретиком квантовой гравитации Джимом Хартлом, которая, как я чувствовал, содержала еще одну деталь пазла. Но, сидя поздним вечером 6 марта 2010 года в своей квартире в Уинчестере, я никак не мог сложить части головоломки. Я решил прогуляться. К моему удивлению, всего через пять минут на холоде у меня в голове наконец-то щелкнуло! Я вдруг понял, как разом решить обе проблемы: объединить два уровня мультиверсов и объяснить неравные вероятности. Это не давало мне уснуть до трех часов ночи и поглотило весь следующий день, который я провел в изумительном, подобном трансу состоянии, которое испытываешь, когда совершенно что-либо понимаешь. Я чувствовал, что это одна из самых замечательных догадок, посетивших меня с момента переоткрытия декогеренции девятью годами ранее, и я не мог остановиться, пока не написал четырехстраничный набросок статьи для Энтони.

Рис. 8.11 иллюстрирует ключевую идею. Допустим, вы собираетесь выполнить эксперимент с квантовыми картами, слегка наклонив карту, так что ожидаете увидеть ее упавшей лицом вверх и выиграть 100 долларов с вероятностью 2/3. В традиционном виде (слева в каждом прямоугольнике на рис. 8.11) вначале имеется одна ваша копия, а затем, после эксперимента, – одна либо две копии, в зависимости от того, коллапсирует волновая функция или нет. Если верна копенгагенская интерпретация, то будет существовать один определенный исход, полученный случайным образом. Если же прав Эверетт, то будет две параллельных вселенных, и каждая содержит по одному вашему экземпляру: одна, в которой вы радуетесь выигрышу, другая – где вы опечалены проигрышем.

Пусть теперь существует мультиверс I уровня ( гл. 6 ), как и предполагает современная космология. Это означает, что бесконечное число неотличимых от вас копий выполняет точно тот же эксперимент на других планетах очень-очень далеко (на рисунке это показано рядом нейтральных смайликов). В своих подсчетах я предположил, что уравнение Шредингера для волновой функции описывает всю совокупность частиц, составляющих все ваши копии и копии эксперимента.

Что в итоге? Если волновая функция коллапсирует, получится один случайный исход для всего бесконечного пространства (мультиверса I уровня), так что вы окажетесь довольным на 2/3 планет и опечаленным на 1/3 – здесь нет ничего удивительного. Если же Эверетт прав в том, что коллапса не происходит, то результатом станет целое бесконечное пространство в квантовой суперпозиции различных состояний, в каждом из которых вы радуетесь на одних планетах и печалитесь на других. А теперь – самое интересное. Все эти состояния пространства оказываются неотличимы друг от друга: вы счастливы ровно на 2/3 бесконечного множества планет! Любая конечная последовательность планет со счастливыми и несчастливыми исходами в одном из этих состояний обнаружится где-то в ином месте пространства в каждом из остальных состояний. Можно подумать, что должны существовать отличающиеся состояния пространства, скажем, такое, где вы счастливы на всех до единой планетах. Однако, опираясь на уравнение Шредингера и математические свойства гильбертова пространства, я смог доказать, что получаемая в итоге волновая функция равна простой суперпозиции бесконечного числа неотличимых состояний. Нас с Энтони по ряду причин это поразило.

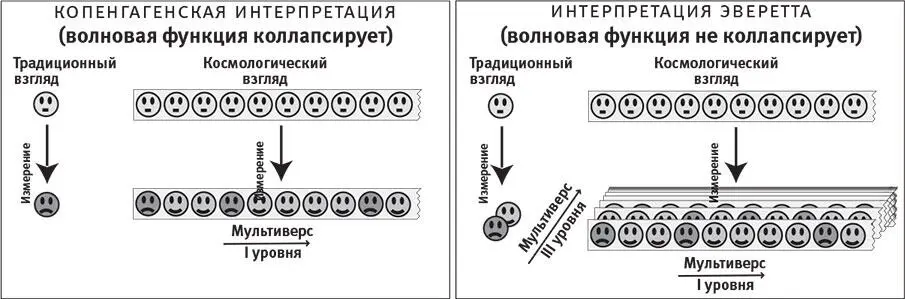
Рис. 8.11.Как объединяются мультиверсы I и III уровней? Каждый кружок – это планета, где вы ставите деньги на то, что квантовая карта упадет лицом вверх. Вначале вы в нейтральном настроении, а после измерения радуетесь выигрышу либо опечалены проигрышем. Карта чуть-чуть наклонена, так что вы ожидаете выиграть с вероятностью 2/3. Эти планеты обычно очень удалены друг от друга, скажем, на гуголплекс метров в разных направлениях, однако я нарисовал их в ряд, чтобы проиллюстрировать идею.

Прежде всего, великая дискуссия о том, коллапсирует ли волновая функция, завершилась великим разочарованием: это попросту не имеет значения. На рис. 8.11 показано, что независимо от того, прав Эверетт или нет, вы будете счастливы на 2/3 планет. На самом деле, обе стороны спора о коллапсе вышли из него изрядно помятыми. В копенгагенской интерпретации спорная концепция коллапса вводится, чтобы избавиться от досадных параллельных вселенных и добиться единственности исхода события, но, как видно из рисунка, это уже не помогает: даже при наличии коллапса получаются параллельные вселенные с обоими исходами. Для интерпретации Эверетта отличительным признаком служили параллельные вселенные III уровня (квантовые), но на рисунке видно, что их можно спокойно игнорировать, поскольку все они неразличимы. В этом смысле мультиверсы уровней I и III объединяются: если имеется бесконечное пространство с мультиверсом I уровня, то можно игнорировать связанные с ним параллельные вселенные III уровня, поскольку на практике все они представляют собой лишь идентичные копии. Не исключено, что III уровень можно объединить и со вторым, но пока мы не смогли это доказать.

Во-вторых, рис. 8.11 демонстрирует происхождение неравных вероятностей, перенося множественные миры Эверетта в наше старое доброе трехмерное пространство. Различные исходы случаются не только где-то в труднопредставимом математическом гильбертовом пространстве, но и где-то очень далеко в нашем собственном пространстве, которое мы исследуем с помощью телескопов. Суть в том, что после того, как карта упала, но до того момента, когда вы открыли глаза, у вас нет способа узнать, какой из множества копий самого себя вы являетесь, поскольку до этого последнего момента все они чувствуют себя субъективно неразличимыми. Поскольку вы знаете, что 2/3 ваших копий, открывая глаза, видят карту лежащей лицом вверх, вам кажется, что вы случайным образом обнаружите ее в этом положении с вероятностью 2/3. Это аналогично тому способу, каким представители французской знати первоначально ввели понятие вероятности для оптимизации своей стратегии в азартных играх. Если в игре вам известно лишь то, что вы окажетесь в одной из множества равновероятных ситуаций (соответствующих, скажем, тому, как перетасована сдаваемая колода), то вы можете считать, что вероятность вашего выигрыша – это просто доля тех ситуаций, в которых вы выигрываете, среди всех возможных.