Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

Очевидно, что мы узнали уже очень много нового: установили, что давление электронов способно поддерживать существование белого карлика, и сумели с определенной точностью предсказать, как меняется радиус звезды с прибавлением или снижением ее массы. Заметьте, что, в отличие от «обычных» звезд, интенсивно жгущих горючее, белые карлики парадоксальным образом уменьшаются с прибавлением массы. Это потому, что добавленная масса идет на увеличение гравитации звезды, заставляя ее сжиматься. На первый взгляд отношения, выраженные в уравнении (5), предполагают, что необходимо добавить бесконечное количество массы, прежде чем звезда сожмется до нулевого размера. Однако этого не происходит. Важно, как мы говорили в самом начале эпилога, что мы постепенно переходим в то состояние, когда электроны размещаются очень плотно, и первостепенную важность обретает специальная теория относительности Эйнштейна, потому что скорость электронов приближается к скорости света. В результате мы должны отказаться в расчетах от законов движения Ньютона, заменив их законами Эйнштейна. В этом-то все и дело.

Мы сейчас обнаружим, что при росте массивности звезды давление, оказываемое электронами, перестает быть пропорциональным плотности, возведенной в степень 5/3; с какого-то момента давление начинает возрастать медленнее, чем плотность. Расчеты мы проведем, но пока можно отметить, что это грозит катастрофическими последствиями для звезды. Дело в том, что при прибавлении массы обычное увеличение гравитации будет сопровождаться меньшим увеличением давления. Судьба звезды зависит от того, насколько меньшим будет это увеличение давления по сравнению с увеличением плотности, если электроны движутся быстро. Итак, настало время выяснить, каким будет давление «релятивистского» газа.

К счастью, нам не нужно выкатывать на сцену громоздкие механизмы теории Эйнштейна, потому что расчет давления в газе, который состоит из электронов, движущихся со скоростью, близкой к световой, производится почти по тем же лекалам, что и для газа, состоящего из «медленных» электронов. Ключевая разница в том, что мы не можем более опираться на уравнение p = mv , так как это становится некорректным. Однако по-прежнему верно, что сила, с которой действуют электроны, равна изменению их импульса. Ранее мы вывели, что флот электронов, отражающихся от зеркала, оказывает давление P = 2 mv × (nv) . Для релятивистского случая можно записать то же выражение, заменив mv импульсом p . Мы также полагаем, что скорость электронов близка к скорости света, так что заменяем v на c . Наконец, чтобы получить давление в звезде, нужно не забывать о делении на 6. Итак, мы можем записать давление для релятивистского газа как P = 2 p × nc / 6 = pnc / 3.

Как и ранее, можем воспользоваться принципом неопределенности Гейзенберга и указать, что, поскольку типичный импульс ограниченных электронов равен h(n/2) ⅓, то

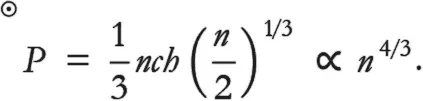
Мы опять можем сравнить этот результат с точным решением, которое выглядит так:

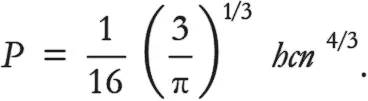
Наконец, можем воспользоваться привычной методологией, чтобы выразить давление через массовую плотность звезды и вывести альтернативу уравнению (4):

где κ' ∝ hc × (Z / (Amp)) 4/3. Как мы и обещали, давление, аналогично плотности, увеличивается медленнее, чем в нерелятивистском случае, а именно: плотность увеличивается со степенью 4/3, а не 5/3. Причина такого замедления кроется в том, что электроны не могут двигаться быстрее скорости света. Это значит, что «векторный» показатель nv , который мы использовали для вычисления давления, перенасыщается в nc , и газ не может перенести электроны к зеркалу (или грани куба), чтобы поддерживалась плотность ρ 5/3. Теперь можно изучить последствия таких изменений, поскольку с помощью тех же рассуждений, что и в нерелятивистском случае, мы можем прийти к аналогу уравнения (5):

Это очень важный результат, потому что, в отличие от уравнения (5), здесь отсутствует какая-либо зависимость от радиуса звезды. Уравнение гласит, что звезда этого типа, переполненная очень быстрыми электронами, может иметь лишь очень конкретную массу. Введя в уравнение вместо κ' выражение из предыдущего абзаца, получим следующее предсказание:

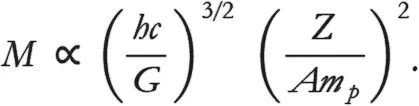
Об этом-то результате мы и говорили в самом начале эпилога как о максимальной массе, которую может иметь звезда – белый карлик. Мы очень близки к тому, чтобы воспроизвести результат Чандрасекара. Остается лишь понять, почему именно это конкретное значение и есть максимально возможная масса.

Мы знаем, что у не слишком массивных белых карликов радиус будет не слишком мал, а электроны – не слишком уплотнены. Таким образом, они не совершают чрезмерных квантовых колебаний, а их скорость по сравнению со скоростью света невелика. Мы знаем, что эти звезды стабильны с отношением массы и радиуса в форме RM ⅓= константа. Теперь представьте, что звезда обретает большую массу. Отношения между массой и радиусом дают понять, что при этом звезда уменьшается, и электроны в результате еще больше сжимаются, а следовательно, перемещаются быстрее. Добавим массы – и звезда еще немного уменьшится. При увеличении массы увеличивается скорость электронов, пока они со временем не начинают двигаться со скоростями, сравнимыми со скоростью света. В то же время давление постепенно изменяется с P ∝ ρ̅ 5/3до P ∝ ρ̅ 4/3, и в последнем случае звезда будет стабильна только при конкретном значении массы. Если масса выше этого конкретного значения, то правая часть выражения κ'M 4/3∝ GM ² больше, чем левая, то есть уравнение оказывается неверным. Это значит, что давления электронов (которое отражено в левой части уравнения) недостаточно, чтобы уравновесить внутреннюю гравитацию (присутствующую в правой части), и звезду ожидает неизбежный коллапс.

Если бы мы более тщательно вычисляли импульс электрона и выкатили бы на сцену высшую математику для подсчета отсутствующих цифр (опять же легкая задача для персонального компьютера), можно было бы сделать точное предсказание максимальной массы белого карлика. Она равна:

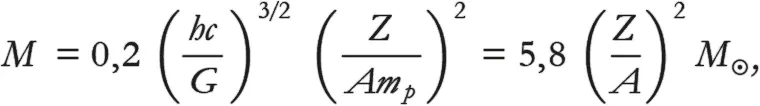
где мы выражаем множество физических констант через массу нашего Солнца ( M ). Заметьте, кстати, что весь дополнительный тяжкий труд, от которого мы отказались, дает в результате всего лишь константу пропорциональности со значением 0,2. Это уравнение и выражает вожделенный предел Чандрасекара: 1,4 солнечной массы, если Z / A = ½ .