Калеб Шарф - Ошибка Коперника. Загадка жизни во Вселенной

Однако лишь в 1761 году, когда после смерти Байеса его друг Ричард Прайс [173] Заслуги Прайса обычно сильно недооценивают: без него идеи Байеса не были бы приведены в пригодный для публикации вид и философски осмыслены. , философ и проповедник, разобрал его архив, было обнаружено, что Байес существенно продвинулся на пути к решению одной из самых наболевших проблем, занимавших центральное место в теме математических «случайностей». Именно Прайс собрал воедино наследие Байеса и спустя два года после его смерти добился, чтобы Королевское общество опубликовало его труды. В результате мы помним Байеса в основном за то, что он решил задачу, которая в то время называлась «обратной вероятностью». В наши дни этот термин используется редко, вместо него чаще употребляется словосочетание «апостериорная вероятность». В последующие десятки и сотни лет многие ученые, в том числе, например, Пьер-Симон Лаплас, независимо открыли и развили подобные понятия, и теперь на них строится почти вся современная наука. Однако имя Байеса стоит особняком и увековечено в названии «Теоремы Байеса» [174] Теорема Байеса. В упрощенном виде она выглядит так: Вероятность А при условии В есть произведение вероятности В при условии А и вероятности А, деленное на вероятность В, где А (например) может быть гипотезой или моделью, а В – данными. , в которой отражена суть его последней и величайшей работы по теории вероятностей.

Формулировка теоремы очень проста. Она позволяет математически вычислить вероятность, что та или иная модель или гипотеза верна, при наличии набора наблюдений. А главное – она сводится к тому, как найти точку зрения, позволяющую адекватно оценить свою уверенность в точности теории или прогноза.

Суть этого фундаментального метода можно пояснить при помощи небольшой аллегории, которую придумал и опубликовал в виде примечания [175] Прайс привел в пример новорожденного ребенка, который наблюдает восходы и закаты Солнца. Мне больше по душе цыплята. к посмертной публикации труда Томаса Байеса его друг Прайс. Перескажу ее своими словами. Жил-был математически одаренный, но, к сожалению, крайне наивный цыпленок. Вылупившись из яйца, он в первый день своей жизни с удивлением обнаружил, что Солнце пересекает небосклон и скрывается из виду. Цыпленок не знает, увидит ли он когда-нибудь снова этот сверкающий диск. Поскольку он обладает аналитическим складом ума (что для цыпленка просто поразительно), то формулирует простую гипотезу: вероятность того, что Солнце появится снова, равна вероятности того, что этого не произойдет, то есть шансы распределяются как 1 к 1 или 50 на 50.

Разумеется, проходит несколько часов, и Солнце восходит. Снова пересекает небосклон и снова исчезает. Цыпленок решает пересмотреть свои ожидания (или уверенность в своих прогнозах). Он наблюдал уже два восхода, однако по-прежнему остается вероятность, что это не повторится, поэтому шансы на третий восход составляют уже 2 к 1 (66,7 %). Со следующим восходом цыпленок снова пересматривает свой прогноз – теперь шансы, что назавтра Солнце вернется, уже 3 к 1 (75 %). С каждым днем цыпленок уверяется в неизбежности восхода все сильнее и сильнее – и шансы на восход все ближе и ближе к 100 %. К сотому утру подросший петушок уверен, что Солнце взойдет, уже на 99 % – и ко всеобщей досаде решает, что можно больше не просыпаться ни свет ни заря, чтобы прокукарекать перед рассветом.

Анализ, который проделал юный петушок, – очень простой пример, однако именно такова суть байесовского подхода к данным и теории. Результаты экспериментов, выводы из новых наблюдений и данных влияют на уверенность в гипотезе, помогают оценить вероятность, что она точна. Однако ученым не всегда было ясно, что имеет смысл оценивать неопределенность численно. Более того, об экспериментах и наблюдениях вообще не было принято думать с этой точки зрения, не принято было делать мир таким местом, где царят вероятности и «уверенность» в том, что правда, а что нет. На то, чтобы подобный подход прижился, потребовалось много времени. Даже такой выдающийся ученый, как Гершель (тот самый, который всего несколько десятков лет спустя размышлял над существованием жизни на других планетах), определенно его не применял. Поэтому мы в огромном долгу перед Байесом и всеми, кто в XVIII веке пытался разобраться, как сделать из неопределенности вероятность по примеру нашего петушка.

Как сам Байес пытался решить эту задачу, видно на примере, который сам он приводил, чтобы сделать свои математические формулы нагляднее. Он предлагал представить себе бильярдный стол (годится любой, но давайте представим себе бильярдный ради исторической точности).

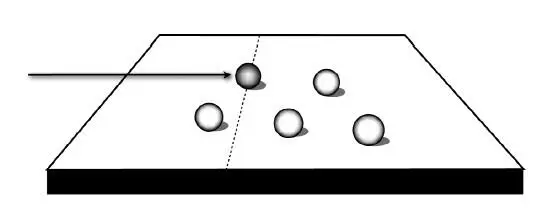
Так вот, представьте себе, что вы небрежно бросаете на бильярдный стол красный шар, который катится себе случайным образом и может остановиться в любом месте. Итак, красный шар остановился в каком-то месте, вы его не трогаете, несколько раз прокатываете по столу в том же направлении белый шар и записываете, как часто он останавливается дальше красного шара. Затем Байес, опираясь на то, где останавливались шары на воображаемом столе, предложил вывести математически обоснованный ответ на следующую простую задачку: если вы знаете, что произошло с теми шарами, которые вы уже прокатили по столу, можно ли предсказать, с какой вероятностью следующий белый шар остановится до или после красного (каковы шансы на тот или иной результат)? Байес показал, что можно. Главное – чем больше прокатишь шаров, тем сильнее будет уверенность в результате следующего броска, в точности как у петушка и Солнца.

Мысленный эксперимент с бильярдными шарами очень прост, однако многое говорит о том, насколько фундаментальным был вопрос вероятностей для математики XVIII века. До того времени никто не разобрался, как проделать необходимые выкладки, а концепции, которые легли в основу работы с неопределенностью, были всем в новинку и даже пугали. Байес двигался к формулировке теоремы, которая впоследствии получила его имя – теоремы, при помощи которой можно было вычислить, насколько человек «верит» в гипотезу перед лицом свидетельств, как правдоподобие в чьих-то глазах или уверенность в чем-то связаны с тем, что то или иное утверждение верно.

Чтобы вам легче было понять смысл теоремы и разобраться, как можно применить ее к нашему вопросу о жизни во Вселенной, приведу чуть более красочный и сложный пример, чем восходы и бильярдные шары. Представьте себе, что у меня есть любопытная гипотеза, что 20 % популяции котов на планете составляют чеширские коты [176] Что именно вдохновило Льюиса Кэролла на создание этих культовых животных (или по крайней мере одного), осталось неизвестным. Гипотез множество – от геральдических львов и церковных горгулий до сказок о всем довольных, напившихся молока котах из английского графства Чешир. . Само собой, чтобы проверить свою гипотезу, я должен пойти и найти какое-то количество котов, выявить среди них чеширских и не-чеширских и посчитать, сколько их. Эта задача не то чтобы разительно отличается от поиска признаков инопланетной жизни – обитаемых и необитаемых планет.