Нейт Сильвер - Сигнал и шум. Почему одни прогнозы сбываются, а другие – нет

К сожалению, эксперимент Ричардсона бесславное провалился {252} – он «предсказал» серьезный рост атмосферного давления, в реальности же в тот день это не наблюдалось. Однако Ричардсон тем не менее опубликовал свои результаты. Этот метод определенно казался правильным методом предсказания погоды – Ричардсон считал, что следует не полагаться на грубые статистические приближения, а выявить некие основные принципы и воспользоваться глубоким теоретическим пониманием поведения системы.

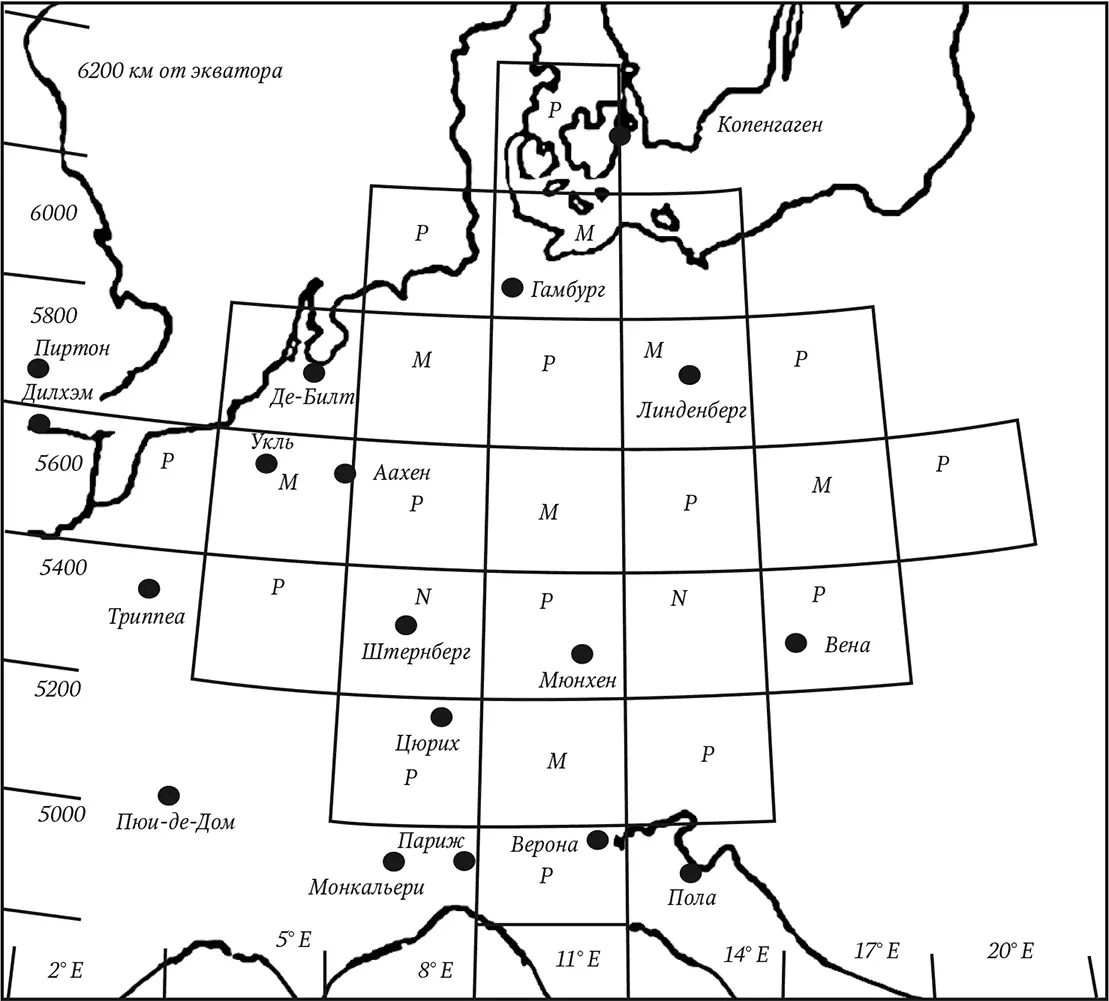
Рис. 4.1.Матрица Ричардсона – прообраз современной системы прогнозирования погоды

Проблема состояла в том, что метод Ричардсона требовал выполнения огромного объема работы. Для решения поставленных им задач были нужны компьютеры. Как вы увидите в главе 9, компьютеры не каждую из поставленных им задач могут выполнить и далеко не всегда служат панацеей в процессе предсказания. Однако компьютеры идеальны с точки зрения вычислений – то есть быстрого и точного многократного повторения одних и тех же арифметических задач. Они отлично подходят для решения шахматных задач, подчиняющихся довольно простым правилам, но сложных с точки зрения вычислений. Сходные задачи имеются и в области метеорологии.

Первый компьютерный прогноз погоды создал в 1950 г. математик Джон фон Нейман, который использовал для этого машину, способную осуществлять порядка 5000 вычислений в секунду {253}. Расчет происходил намного быстрее, чем мог сделать Ричардсон с карандашом и листом бумаги на французском деревенском поле. Тем не менее прогноз оказался неудачным, и его результаты оказались не намного точнее обычной случайной догадки.

Со временем, к середине 1960‑х гг., компьютеры начали демонстрировать определенные навыки в прогнозировании погоды. Так, Bluefire, выдающий результаты примерно в 15 миллиардов раз быстрее, чем первый компьютерный прогноз (и, возможно, в квадрильон раз быстрее, чем Ричардсон), дает нам куда более осмысленные результаты благодаря скорости вычислений.

Прогнозы погоды в наши дни значительно чаще бывают верными, чем 15 или 20 лет назад. Однако, если скорость вычислений в последние десятилетия увеличивалась по экспоненте, прогресс в точности прогнозов погоды был хотя и стабильным, но медленным.

Можно назвать две основные причины сложившейся ситуации. Первая связана с тем, что мир имеет не одно и не два измерения. Самый надежный способ повысить правильность прогноза погоды – то есть на один шаг приблизиться к пониманию поведения каждой молекулы – состоит в уменьшении размера сетки, используемой для отображения атмосферы. Сектора Ричардсона имели размер 340 на 340 км, обеспечивая в лучшем случае слишком масштабный взгляд на планету (в квадрат 340 на 340 км² можно почти полностью вместить Нью-Йорк и Бостон – города, в которых может быть совершенно разная погода). Предположим, вы хотите в два раза уменьшить площадь секторов, до 170 на 170 км. Благодаря этому ваш прогноз станет более точным, но при этом увеличится количество уравнений, которые вам надо решить. В реальности количество уравнений вырастет не в два, а в четыре раза, поскольку вы уменьшаете масштаб и по длине, и по ширине. Иными словами, для того чтобы решить такую задачу, вам нужно примерно в 4 раза увеличить вычислительную мощность.

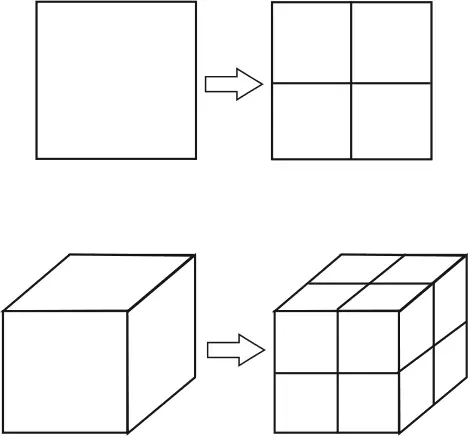
Однако вам нужно учитывать не только эти два измерения. В верхних слоях атмосферы могут проявляться одни закономерности, а в нижних слоях, над океанами и у поверхности Земли – совершенно иные. В трехмерной вселенной двукратное увеличение разрешения нашей сетки потребует восьмикратного повышения вычислительной мощности. Кроме этого, имеется и четвертое измерение – время. Если метеорологическая модель статична, в ней нет никакого толка – самое главное для нас состоит в том, чтобы знать, как меняется погода в каждый момент времени. Шторм движется со скоростью примерно 40 миль в час – если размеры вашей сетки составляют 40×40×40, то вы можете отслеживать его движение, собирая наблюдения каждый час. Однако если вы уменьшите размер сетки до 20×20×20, то шторм будет перемещаться из ячейки в ячейку каждые полчаса . Это значит, что вам нужно уменьшить в два раза и временной интервал, то есть вам потребуется в 16 раз больше вычислительных мощностей, чем изначально.

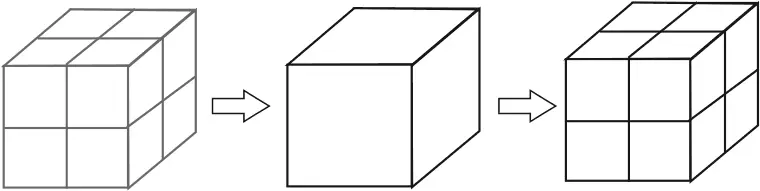
Но если бы эта проблема оказалась единственной, то ее вполне можно было бы решить. Хотя вам нужно, грубо говоря, в 16 раз увеличить вычислительную мощность, чтобы удвоить разрешение прогноза погоды, сама вычислительная мощность растет по экспоненте, удваиваясь примерно каждые два года {254}. Это значит, что вам нужно подождать всего восемь лет, и тогда ваш прогноз станет в два раза точнее; интересно, что NCAR обновляет свои суперкомпьютеры примерно с такой же частотой.

Предположим, что вам удалось разобраться с законами динамики движения жидкостей, которым подчиняются погодные системы. Они в целом следуют ньютоновским законам. Вам не будет особенно мешать и принцип неопределенности, интересный для физиков. Вы получили доступ к компьютерному шедевру типа Bluefire. Вы наняли Ричарда Лофта для проектирования и тестирования компьютерных программ. Что же еще может пойти не так в этом случае?

Итак, с чем может быть связана очередная ваша проблема? С теорией хаоса. Возможно, вам доводилось слышать выражение « взмах крыльев бабочки в Бразилии может привести к торнадо в Техасе» . Изначально это было частью заглавия научной работы {255}, представленной в 1972 г. преподавателем Массачусетского технологического института Эдвардом Лоренцем, который начинал свою карьеру как метеоролог. Теория хаоса применима в отношении систем, для которых справедливы два утверждения:

1) системы динамичны , что означает, что поведение системы в один момент времени влияет на ее поведение в будущем;

2) системы нелинейны , иными словами, в них поддерживаются скорее экспоненциальные, а не аддитивные связи.

Динамические системы доставляют специалистам по прогнозированию немало проблем. Примером может служить описанный в главе 6 факт, свидетельствующий о том, что американская экономика постоянно вызывает цепную реакцию событий, что и является одной из причин, по которым ее развитие так сложно предсказать. Развитие при этом остается нелинейным: ценные бумаги, обеспеченные закладными, стимулировавшие начало финансового кризиса, были разработаны таким образом, что небольшие изменения в макроэкономических условиях значительно повышали риск дефолта по ним.