Эдвард Боно - Курсы развития мышления

Есть и еще одна причина, по которой логика не всегда успешно справляется с задачей. Иногда поиск решения заходит в тупик, и тогда необходима некая свежая идея. Никакая модификация прежних версий не дает нужного ответа. Совершенно новая идея не связана с прошлым опытом. Логика здесь не поможет. Ради справедливости заметим, что к идее, которую один человек воспринимает как абсолютно новую, другой приходит логическим путем, проанализировав ситуацию с иной точки зрения.

Прежде чем перейти к его рассмотрению, обратимся к предварительному тесту возможных комбинаций. Так как блоков шесть, а по условию задачи каждый из них должен касаться пяти других, значит, он будет иметь касание со всеми остальными. Следовательно, любая комбинация, в которой какие-либо два блока не соприкасаются, должна считаться непригодной. Этот простой тест намного проще, нежели подсчет числа контактов каждого блока.

Оба подхода, описанные ниже, являются, по сути, логическими. Это не означает, что метод случайного поиска здесь неэффективен, он просто не был использован. В определенной степени даже логический метод связан с пробами и ошибками на некоторых стадиях решения задачи.

Обычно метод случайного поиска заключается в видоизменении начальной ситуации, пока она не станет удовлетворять нужному решению. Нередко целесообразен и обратный процесс.

Если отложить один блок в сторону, то достаточно лишь скомбинировать пять блоков так, чтобы каждый из них касался остальных четырех. Это первая часть задачи. Вторая: теперь нужно разместить шестой блок, и он должен касаться пяти других блоков. Таким образом, и остальные блоки будут иметь пять контактов (4 + 1 = 5). Для решения задачи сперва используется группа из трех блоков. Еще один блок необходимо расположить так, чтобы он касался этих трех. Это уже комбинация из четырех блоков, где каждый блок касается трех других. Пятый блок нужно расположить аналогично, чтобы он касался всех первых четырех блоков. Одним словом, без оригинальной идеи здесь не обойтись.

Новая идея заключается в размещении блоков по диагонали. Ранее же во всех комбинациях блоки располагались симметрично. Обычно идея диагонального размещения блоков приходит случайно, когда вы пытаетесь передвигать блоки по верху группы из трех блоков. Конечно, вы можете считать, что нашли ее чисто логическим путем.

После того как комбинация из пяти блоков завершена (рис. 15), остается лишь добавить шестой блок и затем переместить три верхних блока так, чтобы они касались всех нижних. Практически нужно сместить два верхних блока вверх и добавить к ним шестой блок.

Совершенно другой подход к решению вытекает из предположения, что наибольшее количество блоков, стоящих на горизонтальной плоскости и образующих один стык, составляет три. Это дает уже известную нам группу из трех блоков. Если одну такую группу поставить на другую (как это сделано в задачах 2 и 3), то останется лишь добиться нужной комбинации стыков. Теперь главное внимание уделяется именно стыкам. Блоки нам на данном этапе не нужны, поскольку они будут скорее мешать, чем помогать. Нарисуем один Т-образный стык блоков, а поверх него другой такой же, чтобы второе «Т» пересекало первое в четырех местах. Это означает, что каждый блок верхней группы будет перекрывать два стыка нижней группы, а следовательно, три блока. Такая комбинация показана на рис. 16.

Окончательное решение задачи 4 изображено на рис. 17.

Сделаем некоторые выводы.

1. Быстрый предварительный тест всех вариантов значительно ускорит процесс решения, особенно если используется метод случайного поиска.

2. Иногда для решения задачи необходим абсолютно новый подход.

3. Новая идея не должна следовать из старых, она приходит «извне» или по воле случая.

4. При решении задачи часто полезно идти от последней ситуации к начальной.

5. Иногда даже при использовании логического метода один из шагов может оказаться случайным.

6. Переключение внимания с одного аспекта задания на другой может привести к нужному решению.

7. Нередко и черновые наброски на бумаге оказываются полезными, даже если задача понятна с самого начала.

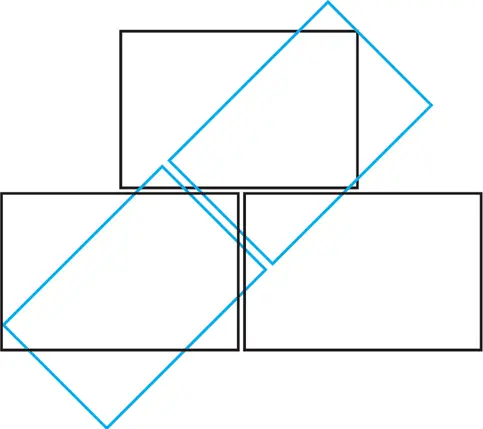
Рис. 15. Комбинация из пяти блоков.

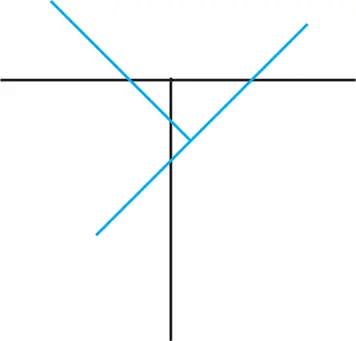
Рис. 16. Т-образный стык блоков.

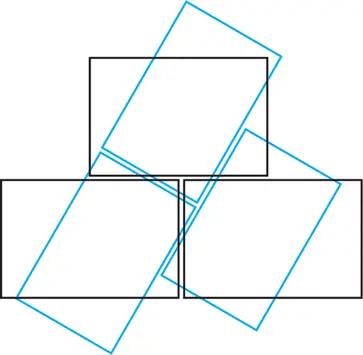
Рис. 17. Решение задачи 4.

Расположите блоки в следующем порядке:

один из блоков должен касаться лишь одного другого;

один – двух других;

один – трех;

один – четырех;

один – пяти остальных.

Эта задача кажется более сложной, чем предыдущая. На самом же деле в ней меньше условий, поскольку ограничения установлены лишь для пяти блоков. Главное отличие здесь – для каждого блока они формулируются отдельно. Вам предстоит узнать, усложняет это задачу или нет.

На первый взгляд, задача подходит для поэтапного решения. Многие люди чаще всего пользуются именно этим методом. Условия задачи удовлетворяются одно за другим, а когда и последнее требование выполнено, задача может считаться решенной. Если подобных требований очень много, то есть задача кажется вам сложной, этот метод особенно эффективен. Хотя, возможно, вы предпочтете другой подход, не расчленяя задачу на части, а пытаясь упростить ее в рамках единого целого.

Недостаток поэтапного решения заключается в том, что многие задачи нельзя решить «по кусочкам». Если все части решения взаимосвязаны, нельзя получить нужный ответ шаг за шагом. Задачи с банками относятся именно к таким.

Другой недостаток рассматриваемого метода: выбор этапов может стать решающим. Неверный их порядок значительно усложняет решение задачи либо делает его невозможным. Выбор верной последовательности действий не всегда является очевидным.

Вместо поэтапного решения можно попытаться упростить задачу. Как? Рассмотреть задачу со всех сторон, пока не выявится в полной мере ее суть.

Задача 5 не связана с предыдущими. Опыт их решения здесь бесполезен.

Ниже приведены возможные шаги при использовании поэтапного метода.

Первое требование: один блок должен касаться лишь одного другого.

Первый шаг: положите на стол один блок и придвиньте к нему второй.

Второе требование: один блок должен касаться двух других.