Эндрю Ходжес - Вселенная Алана Тьюринга

«Существует несколько режимов или стилей, в которых машины могут работать, и каждый из них обладает своими условиями и ограничениями на какие-то определенные операции. Инженеры, к примеру, считают допустимым удаление лампы или временной связи двух точек с помощью зажимов, но будут против применения молотка. Удаление ламп и любые изменения между соединениями не допускаются никем – ни программистами, ни пользователями, более того, для них есть дополнительные ограничения. Так, например, есть разные режимы операций, но здесь мы поговорим только о формальном режиме. В этом режиме достаточно жесткие и строгие условия. Преимуществом работы в таком режиме является то, что результат, записанный принтером, дает полное описание процесса на любом этапе. Детальность такого подхода вкупе с другими документами предоставит каждому ту информацию, которая ему необходима. В частности, такая запись показывает все произвольные выборы человека, который управляет машиной, то есть нет необходимости запоминать последовательность шагов, сделанных в тот или иной момент операции».

Помимо таких сопутствующих исследований в его работе (которая в данном случае предвосхитила появление понятия «операционная система) никто не знал, что именно он делал с машиной, а с осени 1951 года все контакты с остальными пользователями машины и вовсе прекратились.

Алан еще в Принстоне находил особое удовольствие, играясь идеями о шифровании. Так, в одном письме другу он задавался вопросом: «Вы часто спрашивали меня о том, какие возможные применения могут быть найдены для исследований в различных областях математики. Недавно я обнаружил одно из возможных применений той вещи, над которой я в данным момент работаю. Это устройство сможет ответить на вопрос: «Что из себя представляет наиболее общий вид кода или шифра из всех возможных?», и в то же время (естественным образом) позволяет мне создать множество специфических и интересных шифров. Один из них совершенно невозможно взломать без ключа и так же легко позволяет закодировать сообщение. Полагаю, я мог бы продать их правительству Его Величества за довольно внушительную сумму, но я сомневаюсь относительно нравственности такого дела. Что вы об этом думаете?»

Шифрование могло бы стать одним из прекрасных примеров воплощения применимого к символам «определенного метода», действия, которое могло бы выполняться одной из машин Тьюринга. В самом понимании шифрования лежала необходимость, чтобы кодирующее устройство работало, как машина, в согласии с любым правилом, заранее установленным с получателем сообщения.

Что касается «наиболее общего вида кода или шифра из всех возможных», если подумать, любая машина Тьюринга включала в себя процесс кодирования информации, указанной на рабочей ленте, в записанную на ней информацию по завершению выполнения операций. Тем не менее, для практического использования появлялась необходимость в машине обратного действия, которая смогла бы восстановить изначальные данные на ленте. Что бы ни представлял из себя результат работы, она должна была основываться именно на этих принципах. Но относительно «специфических и интересных шифров» он пока в то время еще не смог развить свои идеи.

Идея вернуться к шифрованию появилась в 1937 году. Один из его друзей Малкольм Макфэйл, физик из Канады, писал: «Скорее всего, именно осенью 1937 года Тьюринг с тревогой осознал возможность военного конфликта с Германией. В то время он предположительно усердно трудился над своей известной диссертационной работой и тем не менее нашел время заняться криптоанализом со свойственной ему страстью… Мы много раз обсуждали эту тему. Он предположил, что слова могут быть заменены числами, указанными в официальном словаре кодов, так что сообщения будут передаваться в виде чисел, представленных в двоичной системе исчисления. Но чтобы предотвратить ситуацию, если в руки врага попадет словарь кодов и у него появится возможность расшифровать сообщение, он предложил умножить число в соответствии со специальным сообщением на секретное число с ужасно большим рядом цифр и передать полученный результат. Длина ряда цифр должна была отвечать условию, что у сто немцев, работающих по восемь часов в день за настольными счетными машинами, смогут расшифровать секретный множитель только через сто лет поиска!

Тьюрингу действительно удалось разработать электрическое устройство, выполняющее операцию умножения, и собрал его основную часть, чтобы проверить, будет ли оно выполнять поставленную перед ним задачу. Для этих целей ему потребовались релейные переключатели, которые не было возможности приобрести, и он собрал их сам. Факультет физики Принстонского университета содержал небольшую, но хорошо оснащенную механическую мастерскую для проведения практических работ его аспирантов, и мой незначительный вклад в этот проект заключался в том, что я передал Алану свой ключ от мастерской, что, возможно, противоречило всем правилам устава университета, и показал ему, как пользоваться токарным станком, дрелью, прессом и другими инструментами, – чтобы он не поранил пальцы. Таким образом, он смог собрать и запустить релейные переключатели, и к нашему общему изумлению и восторгу, устройство действительно работало».

С точки зрения математики этот проект не был передовым, поскольку выполнял только операцию умножения. Но даже без применения передовых теоретических знаний оно подразумевало применение «скучной и элементарной» математики, о которой вовсе не было известно в 1937 году.

Прежде всего, представление чисел в двоичной системе исчисления могло показаться новшеством любому, кто занимался практическими вычислениями. Алан же уже давно использовал двоичные числа. Их использование не подразумевало никакого особого смысла, только позволило представить все вычислимые числа в виде бесконечных последовательностей, состоящих из одних нулей и единиц. В устройстве-умножителе, однако, преимущество использования двоичных чисел было очевиднее: в таком случае таблица умножения упрощалась до нижеприведенного вида:

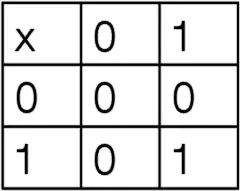
При использовании такой упрощенной таблицы, работа умножителя сводилась к операциям переноса и добавления символов.

Другим любопытным аспектом этого проекта стала его связь с элементарной логикой. Арифметические операции с нулями и единицами могли рассматриваться в рамках логики высказываний. Таким образом, упрощенная таблица умножения, к примеру, могла рассматриваться как эквивалент логической функции «И». Примем p и q за логические высказывания, тогда нижеприведенная “таблица истинности” покажет, при каких условиях высказывание “p и q” будет верным: