Дэвид Сэлли - Игра с числами. Виртуозные стратегии и тактики на футбольном поле

Почему футболисты похожи на прусских коней

Для того чтобы объяснить, как случайность и шанс позволяют нам прогнозировать, что может случиться во время матчей лиги в течение сезона, нам придется сделать одно странное отступление: заглянуть в конюшню прусской военной кавалерии конца девятнадцатого века и познакомиться с мыслями русского экономиста через теории французского математика.

Как и профессиональные футболисты, кавалерийские лошади время от времени взбрыкивают. Когда они это делают, последствия могут быть более серьезными, чем травмы, полученные в стычке на футбольном поле, прусской армии удалось это выяснить за 20 лет начиная с 1875 года. В этот период 196 солдат нашли смерть под копытами своих верных коней. Должно быть, это были абсолютно случайные события: военные должны были достаточно хорошо знать лошадей, чтобы определить, когда боевые лошади пугались, нервничали или оказывались под обстрелом, и армии не было смысла признавать, что ее солдаты систематически допускали ошибки и были сами виноваты в собственных смертях. Нет, каждая смерть была случайной и бессмысленной – например, злосчастный пруссак оказывался не в том месте и не в то время. Никакой закономерности – просто случайность.

Но русский политический экономист польского происхождения Владислав Борткевич в конце девятнадцатого века собрал данные о смертях от копыт лошадей, что позволило по-другому взглянуть на кажущуюся произвольность смертельных случаев 4. Он создал знаменитую таблицу данных с 280 ячейками (14 кавалерийских корпусов на 20 лет), где демонстрировалось ежегодное количество смертей в каждом корпусе. Когда он посмотрел на ячейки, то очень быстро заметил, что их большая часть (51 процент) пуста, это означало, что в данном корпусе в данном году смертей не было. В почти трети ячеек была отмечена одна смерть, в 11 процентах – две, в четырех процентах – три, в двух ячейках – четыре, и ни в одной ячейке не было пяти или более смертей.

После достаточно долгого изучения таблицы Борткевич пришел к выводу, что в, казалось бы, бессистемных случаях есть логика, что в хаотичности есть системность. Проницательность русского ученого подсказала ему воспользоваться формулой распределения случайных величин, выведенной французским математиком Симеоном Дени Пуассоном. В своей работе Recherches sur la probabilitй des jugements en matiиre criminelle et en matiиre civile («Исследование о вероятности приговоров в уголовных и гражданских делах») Пуассон попытался математически описать количество совпадений, которое может произойти, если пара за парой 52 раза переворачивать верхние карты в двух перетасованных колодах 5.

Используя свои данные о кавалерии, Борткевич обнаружил кое-что, чего не заметил француз: распределение Пуассона могло дать начало закону малых чисел, прогнозированию того, сколько раз определенное редкое событие может случиться в заданное время или в заданном месте. Мы можем прогнозировать общую частоту и распределение случайных событий (как часто они происходят и насколько вероятно, что они произойдут), если пытаемся проанализировать событие, которое случается нечасто, но регулярно и достаточно независимо для того, чтобы разработать основной коэффициент 6.

Удар лошадиным копытом является одним из таких событий. По данным Борткевича, смерть под копытами прусских военных коней происходила с коэффициентом около 0,70 на каждый корпус в год. Сочетая эти данные с распределением Пуассона, Борткевич обнаружил примечательное совпадение между действительным распределением смертей и прогнозируемым распределением. Другими словами, формула Борткевича становится для нас способом предсказывать редкие и случайные события.

Что это значит? Это значит, что то, что кажется бессмысленным, случайным, на самом деле обладает предсказуемым характером. Борткевич ничего не знал о качестве сена и травы, о количестве упражнений и тренировок, о параметрах коней или разведении, о любых других параметрах, которые, по вашему мнению, могли бы оказать то или иное влияние. Все, что у него было, – основной коэффициент, информация о том, сколько смертей от ударов копыт происходило каждый год. Хотя мы не можем точно спрогнозировать, когда именно произойдет удар копытом, мы можем с большой вероятностью предположить их общее количество . Редкое и случайное абсолютно прогнозируемо; мы точно знаем, сколько этих случаев произойдет. Случайность логична, как и говорил Кройф.

Статистики применяют распределение Пуассона ко многим редким событиям: попадания «Фау-2» в Лондон во время Второй мировой войны, частота дорожно-транспортных происшествий, радиоактивный распад и т. д.

А имеет ли это какое-нибудь значение для футбола? Да, в точности так же, как удары лошадиных копыт, немецкие бомбы и коэффициент радиоактивного распада, голы редки (насколько редки, мы обсудим позже), но постоянны и независимы. На первый взгляд каждый из них случаен. Если рассматривать каждый в отдельности, они непредсказуемы. И именно это делает их столь восхитительными.

Но если взять среднее число голов за матч – 2,66 для матчей высших дивизионов в Англии, Германии, Испании, Италии и Франции между 1993 и 2011 годами – и применить распределение Пуассона, мы можем рассчитать, сколько игр за последние семнадцать лет были без голов, сколько – с одним голом, сколько – с двумя и так далее. Нам не требуется знать хоть что-нибудь о тактических построениях, тактике, составах команд, травмах, тренере или болельщиках, ни о чем из этого, чтобы обнаружить, что голевые моменты обладают структурой. Возможно, футбол вероятностный, но все же прогнозируемый.

Эта прогнозируемость означает, что, если говорить о следующем сезоне Премьер-лиги, мы знаем, что около тридцати матчей закончатся без гола, в семидесяти будет забит всего один гол, в девяноста пяти будет в целом два гола, в восьмидесяти – три, в пятидесяти пяти – четыре, а в пятидесяти по-настоящему замечательных матчей будет забито пять или более голов.

Как мы это узнали? Итак, в сезоне 380 матчей и команды забивают около 1000 голов. Благодаря тем самым лягающимся лошадям, французскому математику и русскому экономисту у нас есть все, что необходимо знать, чтобы извлечь логику из случайности.

Распределение Пуассона также может применяться к отдельным результатам матчей.

ДИАГРАММА 5

РАСПРЕДЕЛЕНИЕ СМЕРТЕЛЬНЫХ УДАРОВ КОПЫТАМИ ПРУССКИХ ВОЕННЫХ КОНЕЙ

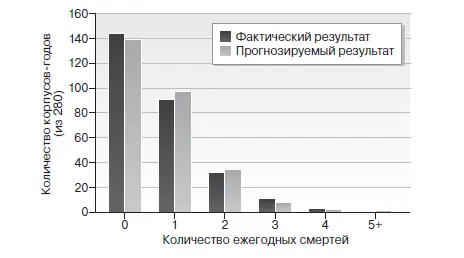
ДИАГРАММА 6

РАСПРЕДЕЛЕНИЕ ГОЛОВ В ЕВРОПЕЙСКОМ ФУТБОЛЕ, 1993–2011 ГГ.

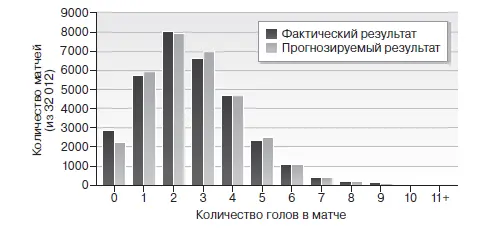
Возьмем среднестатистическую субботу Премьер-лиги. 7 ноября 2010 года результаты матчей были следующими: 2:2, 2:1, 2:2, 4:2, 1:1, 2:1, 2:0. Ничего экстраординарного, но насколько обычными окажутся эти результаты, если мы сравним их со многими субботами во многих сезонах нескольких лиг? Являются ли победы «Манчестер юнайтед» и «Блэкберна» со счетом 2:1, зарегистрированные в этот день, более вероятными, чем победа «Сандерленда» над «Стоком» со счетом 2:0?