Георгий Гамов - Занимательная математика

Логическое умозаключение мисс Аткинсон допускает обобщение на случай, когда в купе находятся более трех пассажиров и лица у всех испачканы сажей. Действительно, четвертый пассажир, обладающий еще более развитыми способностями к логическому мышлению, чем мисс Аткинсон, мог бы рассуждать следующим образом:

— Если мое лицо не испачкано сажей, то трое моих попутчиков должны смеяться друг над другом. Но по крайней мере у одного из них хватит ума, чтобы сообразить, что если бы его лицо не было испачкано сажей, то двое других пассажиров смеялись бы друг над другом и, если они не круглые идиоты, должны были бы понять, что их лица испачканы сажей.

И т. д., и т. д.

Во время нацистской оккупации Франции в купе поезда, шедшего из Парижа в Марсель, ехало четверо пассажиров. Компания подобралась пестрая: молодая очень красивая девушка, пожилая почтенная дама, немецкий офицер и француз средних лет неопределенной профессии. Все четверо не были знакомы друг с другом, и в купе поезда, мчавшегося на юг, царило молчание. Когда поезд въехал в туннель, свет в купе погас, и на несколько минут четверо пассажиров оказались в кромешной темноте.

Внезапно раздался звук поцелуя, за которым послышался мощный удар: судя по всему, кто-то из пассажиров основательно «приложил» кого-то из попутчиков. Когда поезд вырвался из туннеля, все четверо пассажиров с невозмутимым видом сидели на своих местах, и только у немецкого офицера под глазом наливался огромный синяк.

— Так ему и надо, — подумала пожилая дама. — А девчонка молодец! Настоящая французская девушка, умеющая постоять за себя и дать отпор этим наглым бошам! Побольше бы таких девушек!

— Странный вкус у этого немецкого офицера. — размышляла молодая француженка. — Вместо того чтобы поцеловать меня, он предпочел поцеловать эту старую грымзу! Непостижимо!

Немецкий офицер, прижимая носовой платок к пострадавшему глазу, над которым назревал огромный синяк, также не мог никак понять, что произошло в темноте.

По-видимому, этот француз попытался поцеловать девушку, — подумал он, — а та в темноте промахнулась и ударила меня.

Спрашивается, что думал француз и что произошло в действительности?

Хотя некоторые читатели, возможно, сочтут, что эта задача не может быть отнесена к числу математических задач-головоломок, тем не менее она допускает единственное решение. Француз, бывший членом одной из подпольных групп Сопротивления, был очень горд своей выдумкой.

Спору нет, немцы очень умны, размышлял он, но офицер ни за что не догадается, что я поцеловал тыльную сторону своей руки, а потом вмазал бошу кулаком по его мерзкой роже!

После того, как Германия проиграла войну, экономическая ситуация в стране стала быстро ухудшаться. Все продукты были строго нормированы, а самый главный продукт питания, хлеб, выдавался из расчета 200 г на душу населения в день. Все пекари получили строжайшую инструкцию изготовить специальные формы для выпечки 200-граммовых хлебцев — по 1 хлебцу в день на каждого из окрестных жителей.

Старый профессор Карл Z. каждое утро по дороге в университет заходил в булочную, чтобы купить дневную порцию хлеба. Однажды он заявил булочнику:

— Бесчестный вы человек! Вы обманываете своих покупателей!

Ваши формы на 5 % меньше, чем должны быть для выпечки 200-граммовых хлебцев, а сэкономленную муку вы продаете на черном рынке!

— Помилуйте, гepp профессор! — возразил булочник. — Никто и никогда не выпекал хлебцы одного и того же размера. Одни хлебцы получаются на несколько процентов меньше нормы, другие — на несколько процентов больше.

— Вот именно! — подтвердил профессор. В течение нескольких месяцев я ежедневно взвешивал хлебцы, которые покупал у вас, на точных весах в моей лаборатории. Разумеется, результаты взвешивания дали естественный разброс. Вот график, на котором показано число хлебцев различного веса по сравнению с правильным весом (нормой).

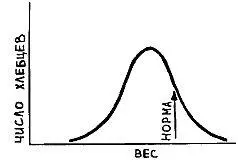
Как видите, одни хлебцы весят всего 185 г, другие — целых 205 г, но средний вес (среднее арифметическое всех измерений) равен 195 г, вместо положенных 200 г. Вам нужно срочно изготовить новые формы для хлебцев правильных размеров, иначе я буду вынужден сообщить о вас властям.

— Разумеется, я изготовлю новые формы завтра же, герр профессор! — пообещал перепуганный булочник. — Смею заверить вас, что ошибка больше не повторится.

Через несколько месяцев профессор Z. снова обратился к булочнику.

— Я сообщил о вас властям сегодня, — сказал профессор. — Вы не изменили формы и продолжаете обманывать своих покупателей.

— Но герр профессор! — воскликнул булочник. — Уж теперь-то вы не можете обвинять меня в том, что я обманываю покупателей. Разве в хлебцах, которые вы покупали у меня за последние несколько месяцев, был недовес?

Недовеса не было. Все хлебцы были весом в 200 г или тяжелее. Но объяснялось это не тем, что вы изготовили формы больших размеров, а тем, что отбирали для меня хлебцы покрупнее.

— Ну, этого вы никогда не сможете доказать! — презрительно процедил булочник.

— Еще как смогу! — возразил профессор Z. — Вот какое статистическое распределение я получил, взвешивая хлебцы, купленные у вас за последние несколько месяцев:

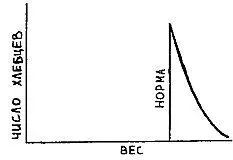
Вместо стандартного распределения ошибок, открытого великим немецкие математиком Карлом Фридрихом Гауссом, получилась сильно искаженная кривая, обрезанная слева и медленно спадающая справа.

Статистические отклонения от среднего не могут привести к такому распределению. Ясно, что оно создано искусственно тем, что вы отбирали для меня хлебцы весом от 200 г и более. Кривая, которую вы видите, хвост гауссова распределения, т. е. того самого распределения, которое я получил, взвешивая хлебцы перед нашим первым разговором.

Не сомневаюсь, что власти, отвечающие за распределение продуктов, прислушаются к моему сообщению.

И повернувшись на каблуках, профессор Z. вышел из булочной.

Юный Николас очень хотел стать членом «Клуба любителей шахмат и шашек» своего города, но в клуб принимали только взрослых.