Георгий Гамов - Занимательная математика

Сэм-младший тоже рассмеялся:

— Что верно, то верно! А если оба бросания завершатся одинаковыми исходами, то их нужно просто исключить и бросать монетку снова два раза подряд. В зачет идут только те бросания, при которых сначала выпадает орел, а потом решка, или сначала решка, а потом орел. Тогда лектор выставляет оценку «отлично», если первым выпадает орел, и «хорошо», если первой выпадает решка.

Причина, по которой такая тактика дает правильный результат, очень любопытна, — продолжал Сэм-младший, и я хотел бы пояснить, в чем тут дело.

Путь рвероятность выпадения орла при первом или втором бросании. Тогда вероятность выпадения решки равна 1 — р. Следовательно, вероятность выпадения в первом бросании орла, а во втором решки равна произведению ри 1 — р, т. е. р(1 —р).

Точно так же вероятность выпадения при первом бросании решки, а при втором орла равна (р — 1)р.

Но так как умножение обыкновенных чисел коммутативно, т. е. произведение не зависит от порядка сомножителей, оба произведения равны:

р(1 — р) = (1 — р)р.

Поэтому твой ответ правилен.

Сэм-старший улыбнулся и сказал:

— Я знал, что когда дело дойдет до денег, я смогу показать тебе, что разбираюсь в своем деле.

— Никогда в этом не сомневался, — заверил отца Сэм-младший. — Я только хотел обратить твое внимание на некоторые тонкости в простейших понятиях теории вероятностей. В том деле, которым ты занимаешься, приходится думать не только о вероятностях, но и о многом другом, например основательно разбираться в теории игр: ведь то, что ты делаешь, по существу сводится к разработке стратегий.

— Ничего подобного! — запротестовал Сэм-старший. Просто у меня большой опыт в тех делах, которыми я занимаюсь, только и всего.

— Никто не спорит и не ставит под сомнение, что ты можешь действовать интуитивно. Но твои приемы есть не что иное как методы теории игр. Если не возражаешь, я попытаюсь продемонстрировать это на очень простом примере.

Предположим, что мы играем с тобой в нехитрую игру. Каждый из нас бросает свою монету. Если обе монеты выпадают вверх орлами или вверх решками, то выигрываешь ты. Если монеты выпадают по-разному, одна вверх орлом, другая вверх решкой, то выигрываю я, причем безразлично, чья именно монета выпадает вверх орлом, а чья вверх решкой. А теперь сделаем игру более интересной.

Если выигрываешь ты, то я плачу тебе 9 пенсов за два орла и 1 пенс за две решки. Если же выигрываю я, то при любом раскладе, т. е. независимо от того, выпадает ли комбинация «орел-решка» или «решка-орел», ты платишь мне 5 центов.

Перед игрой и даже во время игры ты можешь как угодно менять свои монеты на фальшивые.

Как видишь, все сказанное делает игру с бросанием монет гораздо интереснее. Она позволяет выработать удобную стратегию. Поскольку наибольший выигрыш тебе сулит выпадение комбинации «орел-орел», ты можешь предпочесть заменить свои монеты такими, которые чаще выпадают вверх орлом. Но поскольку мне об этом известно, я могу пойти на замену своих монет такими, которые чаще выпадают вверх решкой, так как я выигрываю при выпадении комбинаций «орел-решка» и «решка-орел».

Таким образом, перед каждым из нас возникает проблема: как лучше всего построить схему замены своих монет фальшивыми, если известно, что партнер вырабатывает для себя аналогичную схему.

— Что и говорить, звучит заманчиво, — вынужден был признать Сэм. Так как в среднем я мог бы каждый раз выиграть среднее между девятью центами и одним центом, а ты среднее между пятью и пятью центами, т. е. столько же, сколько и я, мы имеем равные шансы на выигрыш, и я считаю игру честной. Я готов сыграть с тобой и уверен, что сумею заменить свои монеты фальшивыми так, чтобы перехитрить тебя и научить хотя бы немного уважать старших.

Сэм-младший покачал головой.

— Не сердись, но я не возьму твоих денег. Дело в том, что игра, которую я тебе предлагаю, мошенническая: я могу выбрать такую стратегию замены монет фальшивыми, что при достаточно длинной серии бросаний ты можешь лишь надеяться свести проигрыш до минимума. Но ты непременно проиграешь, а я выиграю. Более того, я могу математически вычислить, какую долю бросаний у меня составит выпадение орла независимо от того, выпадает у тебя орел или решка. И из вычислений я могу узнать, сколько смогу выиграть при достаточно длинной серии бросаний.

Я покажу тебе, как производятся такие вычисления, хотя ты можешь поверить мне на слово. Просто мне кажется, что тебе будет интересно. Вот как это делается.

Напомню, что я хочу вычислить долю бросаний, в которых у меня должен был бы выпасть орел. Обозначим ее через х, а размеры моего платежа через Р.

Рассмотрим сначала, что происходит, когда у тебя выпадают орлы. Всякий раз, когда моя монета падает вверх орлом и у тебя выпал орел, я теряю 9 центов. Так как доля орлов составляет хот общего числа бросаний, это означает, что в моей платежной функции есть член — 9х. Аналогичным образом, всякий раз, когда у меня выпадают решки, а у тебя орлы, я выигрываю 5 центов. Так как решки составляют (1 — х)часть от всех бросаний, в моей платежной функции должен быть член 5(1 — х).

Таким образом, если я запишу мою полную платежную функцию для тех случаев, когда у тебя выпадают орлы, то она окажется

Р орлы= -9x + 5(1 — х),

или просто

Р орлы= -14x + 5.

Вот ее график:

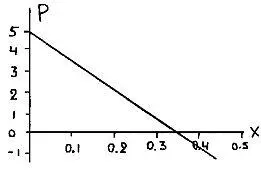
Рассмотрим теперь, что происходит, когда у тебя выпадают peшки. Действуя так же, как прежде, я получаю платежную функцию

Р решки= +5х — 1(1 — х),

Р решки= 6x — 1.

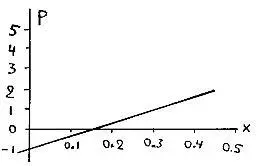
Накладывая оба графика один на другой, мы находим, что они пересекаются при х= 0.3 и Р= 0,8.

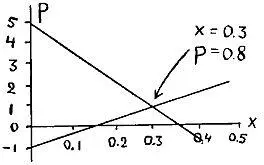
Это означает, что если я заменю 3/10 моих монет на фальшивые и случайным образом распределю фальшивые монеты среди моих монет, то в достаточно длинной серии бросаний я буду в среднем выигрывать 0.6 цента всякий раз, когда твоя и моя монеты выпадут обе либо вверх орлами, либо вверх решками.

— Придумано хитро, хотя, должен признаться, я никак не возьму в толк, как же все получается, — признался Сэм-старший. — Сегодня вечером я собираюсь заглянуть в клуб. Кстати, нет ли у тебя подходящей математической задачки с неожиданным решением? Мне бы хотелось немного позабавиться и позабавить членов клуба.