Дмитрий Лесной - Русский преферанс

Есть такой простенький шулерский приём, называемый приписывание . Думается, что он даже и расшифровки особой не требует. Казалось бы чего проще — записывая, иногда чуть-чуть прибавляешь. Приписывание, однако, требует определённого навыка, известной техники и психологической продуманности.

В старину было много всяких «примочек», таких как двойной мелок, которым игрок записывал при выигрыше один куш, а как бы невзначай прибавлялось два. Здесь главное — не перегнуть палку и не приписывать лишнего в каждой сдаче.

Компьютерная эра все эти проблемы благополучно разрешила. Машина честна и беспристрастна, а главное, не ошибается в арифметике.

Редко кто задумывается над тем, сколько «стоит» конкретно тот или иной шулерский приём. Пожалуй, даже не сразу понятно, что автор имеет в виду, вводя понятие стоимости. На самом деле, ничего удивительного в стоимости шулерского приёма нет. Например, когда человек говорит: «Знал бы прикуп — жил бы в Сочи», его можно спросить, по какой ставке и в какую пульку он играл бы, после чего несложно вычислить его средний предполагаемый доход, причём достаточно точно. Известно, что знание прикупа в сочинском гусарике приносит знающему в среднем 200 вистов в пульке до 50.

Иногда доходность шулерского приёма можно вычислить с точностью «до копейки». Потому что любой шулерский приём призван изменить вероятность выигрыша. А теория вероятностей — наука точная. Для иллюстрации рассмотрим пример с игральными костями. Один человек бросает две шестигранные игральные кости, а другой делает ставку на то, что выпадет комбинация 6–6.

Подсчёты в играх с костями даже как-то неловко называть математикой . Точнее было бы назвать их арифметикой, потому что они очень просты. Тем не менее жизненный опыт показывает, что многие люди, играющие в игры с костями (например, в нарды), зачастую имеют весьма поверхностное (а иногда и превратное) представление о вероятностях выпадения различных комбинаций. Между тем точное представление именно об этой стороне дела является основой класса игрока в любой игре, в том числе и карточной.

Итак, одна игральная кость (представляющая собой кубик правильной формы, все грани которого равны) [251]может с равной вероятностью выпасть любой из своих шести граней. Что будет, если мы станем держать пари на то, что выпадет именно шестёрка ? Чтобы игра была равной, противник должен «отвечать» пятикратным, т. е. за нашу ставку 1 доллар платить в случае выпадения шестёрки 5 долларов, потому что у него ровно в пять раз больше шансов, что шестёрка не выпадет. Если кинуть кубик шесть раз и все шесть раз выпадут разные грани, то мы один раз выиграем (5 долларов) и пять раз проиграем (по 1 доллару), оставшись в результате при своих.

Теперь посмотрим, что будет, если мы бросаем сразу два кубика. На каждую из шести граней первого кубика приходится шесть граней второго. Число возможных сочетаний граней составляет 36 — шесть в квадрате. Все они представлены в табл.1. Представим, что мы держим пари за то, что выпадет определённая комбинация, например 6–6. Какова должна быть выплата за 6–6, чтобы игра была равной? Тот же порядок рассуждений: единственной из 36 возможных комбинаций (6–6) противостоит 35 других, при выпадении которых мы проиграем. Соответственно выплата должна составлять 35:1.

Таблица 1. Возможные сочетания гранейЗдесь кроется небольшой подвох, губительный для всех, кто о нём не знает. Дело в том, что вероятность выпадения комбинации 6–5 в два раза выше, чем 6–6 . Фактически комбинаций 6–5 две, а не одна: первый кубик (представим, что он красного цвета) выпал шестёркой кверху, а второй (пусть он будет синим) — пятёркой; красный — пятёркой, а синий — шестёркой.

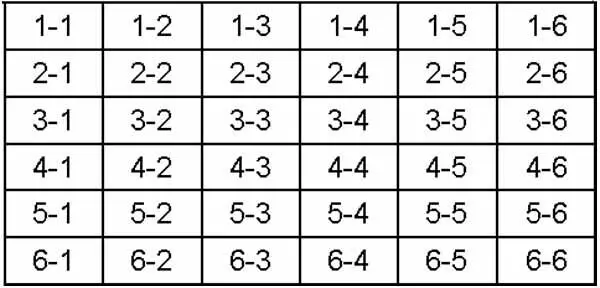
В обоих случаях выпадает как бы одна визуально различимая комбинация 6–5. На самом деле их две, точнее, эта комбинация может быть образована двумя различными способами. Это хорошо видно в табл.1: в правом нижнем углу таблицы с комбинацией 6–6 соседствуют две: 5–6 и 6–5. В игре одинаковыми кубиками эти комбинации внешне не различимы, но вероятности их появления отличаются в два раза. Возьмите пару кубиков и побросайте их, чтобы убедиться, что 6–5 выпадает примерно в два раза чаще, чем 6–6.

Какой же должен быть правильный ответ (т. е. выплата за выпадение комбинации 6–5), чтобы игра была равной? Ответ очевиден: 34:2=17:1.

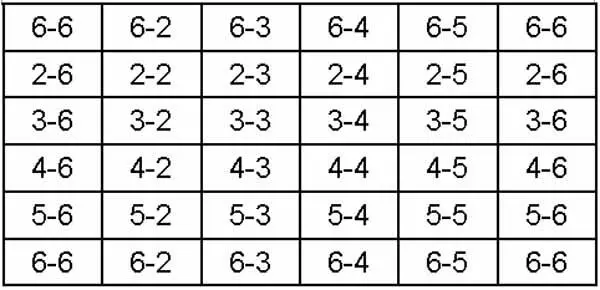
Теперь вернёмся к нашему примеру: игрок ставит на выпадение 6–6, а банкомёт отвечает 35-кратным. С точки зрения математики игра совершенно равная. Повлиять на её исход может только счастье. Но представим, что игрок подменил банкомёту «честные» кости «нечестными». На каждой из шулерских костей две грани помечены как «шестёрка», зато нет ни одной «единицы». (На правильно размеченных игральных костях эти грани противоположны. Поэтому при выпадении цифры 6 на верхней грани вторая «шестёрка» будет не видна.) Теперь наша табличка возможных сочетаний граней будет выглядеть иначе (табл. 2).

Таблица 2. Возможные сочетания граней с использованием шулерских костейВопрос о возможности быть уличённым в подмене оставим пока за скобками. Как видим, комбинаций 6–6 вместо одной стало четыре. Что произойдёт, если игра продолжится? За 36 кидков ду-шеш, по теории вероятностей, выпадет четыре раза и 32 раза выпадут другие комбинации. Игрок 32 раза заплатит банкомёту по 1 доллару и четыре раза получит по 35 долларов, т. е. наживёт за 36 кидков 140-32=108 долларов. Легко сосчитать, что доходность этой игры составляет для игрока 108:36=3, т. е. 3 доллара с каждого броска.

Если игроки будут играть в такую игру долго по одной и той же ставке и сделают, скажем, 1000 бросков, то, по теории, понтёр должен выиграть у банкомёта 3000 долларов.

С картами дело обстоит точно так же. Представим, что игра заключается в том, чтобы угадать достоинство верхней карты в колоде. Если это преферансная колода, то вероятность угадать составляет 1/8 (4/32). При справедливой игре отгадывающий должен получать семикратный ответ.

Представьте теперь, что игрок похитил из колоды банкомёта двух тузов. И всё время называет какие-то карты, отличные от тузов. Вероятность появления любой карты (не туза) составляет в этих условиях 4/30. Чтобы игра была равной, банкомёт должен платить при угадывании 26 к 4. А он платит 28 к 4, т. е. фактически переплачивает полкуша при каждом угадывании. В серии из 30 испытаний он переплатит 2 доллара при игре по 1 доллару. Таким образом, доходность этой игры можно оценить как 1/15 ставки в пользу игрока.