Ерусалимский Львович - Экстерьер собаки и его оценка

Отрезок называется разделенным в среднегармоническом отношении, если его большая часть относится к меньшей так же, как весь отрезок относится к своей большей части (рис. 122). Это приводит к появлению пропорции: 1:Х = Х:(1-Х).

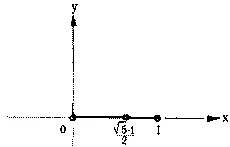
Положительный корень соответствующего квадратного уравнения соответствует координате искомой точки. Обычно пользуются его приближенным значением 0,618 для определения длины большей части отрезка, тогда на долю меньшей части приходится 0,382.

Рассеченный в этом отношении отрезок отличается названным выше свойством — особенной соразмерностью своих трех частей — меньшей, большей и целого, воспринимаемых глазом как внутренне уравновешенных. Вслушаемся в название этого принципа по Евклиду: деление отрезка в среднегармоническом отношении. Тема гармонии уже тогда, за 3 века до нашей эры, с очевидностью была обнаружена, правда, пока еще в одномерном пространстве — на прямой.

Оказалось, что и при выходе в пространство большей размерности принцип, указанный Евклидом, по-прежнему создает гармоничное целое, если трехчастность его формы подчиняется действию евклидовой пропорции.

Мы уже упомянули пример хорошо сложенного человека, у которого горизонтальная линия, проведенная через пупок, отвечает среднегармоническому сечению. Это давало скульпторам и художникам один из гармонических канонов для определения правильных продольных пропорций человеческого тела. Впоследствии выяснилось, что идеальное строение человека и в целом, и в деталях подчиняется евклидову числу и соответствует классическим представлениям о красоте (Фидий, и в честь его Φ = 1/ X, где X — число Евклида).

Приведем отдельные примеры.

Форма головы воспринимается художником совершенной, если отношение ее поперечного и продольного диаметров в точности соответствует евклидову числу (вспомним овал лица, который есть не что иное, как продольное сечение яйца, рис. 123).

Канон женской красоты (рис. 124) определяется отношением талии к бюсту, равным отношению талии к бедрам и равным числу Евклида.

Канон мужской красоты (рис. 125) определяется этим же числом по-другому: здесь евклидовой пропорции соответствует отношение ширины в бедрах к ширине в плечах.

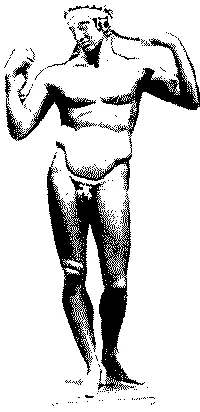
Внимательный читатель сразу усмотрит в этом проявление полового диморфизма и найдет соответствующее функциональное объяснение.

Оказывается, что под действие евклидова сечения подпадает не только гармония человека: всемирно известные архитектурные строения своими пропорциями также повторяют это число (пирамиды Хеопса, Хефрена и Микерина, Парфенон, театр Диониса в Афинах, церковь Покрова на Нерли, храм Василия Блаженного, церковь Вознесения в Коломенском, система «Модулор» Ле Корбюзье…), ему соответствуют примеры из самых неожиданных областей, о которых мы расскажем позже.

И во всех воплощениях, живых и неживых, форма, рождаемая принципом Евклида, вызывает ощущение гармонии, содержащей в себе внутреннее движение, гармонии напряженной, являющейся антиподом гармонии покоя. Таким образом, наряду с буквальной законченностью симметричной формы и ее статичным равновесием возникает парадоксальная завершенность внутренне напряженной формы, сбалансированность частей которой определяется принципом среднегармонического сечения.

Позже этой темой заинтересовались в эпоху Возрождения. Перу ЛУКИ ПАЧОЛИ ди Борго (XVI век), ученого монаха францисканца, принадлежит книга «La proportia Divina» — «Божественная пропорция» с изложением 12 свойств пропорции, являющейся, по мнению автора, «эстетическим законом» природы и искусства. Леонардо да Винчи, иллюстрировавший эту книгу, переименовал «божественную пропорцию» в «золотое сечение» («sectio aureo»).

Так возникло новое, ставшее общепринятым, название указанного Евклидом и ставшего знаменитым принципа деления отрезка в среднегармоническом отношении.

Как и мастера Древней Греции, их наследники эпохи Ренессанса широко пользовались принципом золотого сечения в своих творениях, принадлежавших к самым различным областям искусства, будь то архитектура, скульптура или живопись, и достигали совершенства в поисках гармонии.

На золотое сечение в разные эпохи обращали внимание и ученые.

Великий ученый Средневековья И. Кеплер (XVI век) представил модель Солнечной системы в виде последовательно вложенных друг в друга 5 правильных многогранников, возможность построения которых на основе принципа среднегармонического деления была показана еще Евклидом.

Интерес к золотому сечению привел четырьмя столетиями позже наших современников к неожиданным открытиям в самых разных областях: в явлениях сенсорной сферы человека (И. А. Рыбин), в физиологических ритмах человека, параметрах его «вхождения» во внешнюю среду (В. И. Коробко), в механизме роста и формирования в живой природе (закон преобразования спиральных симметрии, О. Я. Боднар), в музыкальной гамме (В. В. Очинский), в строении и ритмике Солнца (П. К. Бутусов, В. Г. Буданов, Н. Н. Якимова), наконец, в вопросе о целостности мироздания (М. А. Марутаев и его открытие связи между Φ и 137 — числом-следствием фундаментальных констант природы — заряда электрона, скорости света и постоянной Планка)…

Интерес к золотому сечению при изучении учеными высоких материй существовал параллельно практическому интересу инженеров и строителей, вызванному особой прочностью «золотых конструкций», соседствовал с преклонением художников перед совершенной красотой этих конструкций.