Дарья Нестерова - Энциклопедия лучших игр со словами и цифрами

Учитывая все отмеченное выше, чтобы выиграть, нужно назвать числа 299, 19 или 9. В этом случае соперник не выиграет.

Вы знаете простую игру в крестики-нолики? Если да, то вы без труда освоите и ее усложненный вариант. Прежде чем начать игру, вам следует начертить на листке бумаги в клетку поле 5 ? 5.

На игровом поле игроки ставят по очереди в любую клетку крестик или нолик.

Тот, кому удалось поставить три одинаковых знака в ряд (по горизонтали, вертикали или диагонали), побеждает.

Если это не удалось никому из игроков, игра считается сыгранной в ничью.

Подсказка: выигрышная стратегия – соблюдать симметрию.

Это достаточно сложная игра, больше подходящая для проведения математических олимпиад. Однако, если вы обладаете незаурядными математическими способностями и можете найти достойного соперника, вы интересно и с пользой проведете время.

Условие

Игроки ходят по очереди. Один называет два числа, являющиеся концами отрезка. Соперник называет два других числа, являющиеся концами отрезка, вложенного в предыдущий. Игра может продолжаться бесконечно долго.

Первый игрок стремится, чтобы в пересечении всех названных отрезков было хотя бы одно рациональное число, а противник старается ему помешать.

Подсказка: каждым своим ходом второй игрок может избежать того, чтобы определенные рациональные числа попали в пересечение всех отрезков.

Решение

Чтобы выиграть в этой игре, следует соблюдать правильную стратегию. Первым своим ходом необходимо выбрать такой отрезок, чтобы в нем не было ни одной целой точки вида g/2, где g – целое число.

Соблюдая такую стратегию, на n-ом ходу следует выбрать такой отрезок, чтобы в нем не было ни одной точки вида g/n, где g – целое число. При любой игре соперника вы можете выбирать отрезки согласно изложенным выше правилам.

А теперь попробуем доказать, что в пересечении всех названных отрезков не может быть ни одного рационального числа. Итак, пусть рациональное число s/d (для некоторого целого числа s и натурального числа d) лежит в пересечении всех отрезков. Но это противоречит тому, что игрок на d-ом ходу назвал отрезок, не содержащий рациональных чисел, представленных в виде дроби со знаменателем d.

Эта игра довольно сложная. В нее следует играть вдвоем. Для игры потребуется лист бумаги, а также ручки с синим и зеленым стержнями.

Условие

Игроки ходят по очереди. Первый ставит на листе бумаги зеленую точку, второй ставит на свободные места 10 синих точек. После этого первый игрок опять ставит на свободное место зеленую точку, второй ставит на свободные места 10 синих точек и т. д.

Первый игрок считается победителем, если 3 зеленые точки образуют правильный треугольник. Если второй ему помешает, то, соответственно, выигрывает он.

Подсказка: первому игроку следует ставить до определенного момента точки на одной прямой.

Решение

Предположим, первый игрок ставит точки на одной прямой, заботясь только о том, чтобы не попасть в уже поставленную точку (это всегда возможно, поскольку на прямой бесконечно много точек).

Если уже поставлено s зеленых точек на прямой, прибавление еще одной точки на этой прямой только увеличивает количество мест, на которые можно поставить зеленую точку так, чтобы с уже поставленными она образовала правильный треугольник.

Итак, число мест, куда можно поставить точку, чтобы получился правильный треугольник, после постановки (s + 1)-й зеленой точки равно сумме арифметической прогрессии 2 + 4 + 6 + ... + 2s = s(s + 1).

Число синих точек после этого хода станет равным 10(s + 1), что при s > 10 уже меньше, чем число возможных мест для зеленой точки, создающей правильный треугольник.

Учитывая все сказанное выше, можно сделать вывод, что у первого игрока всегда есть возможность после 10-го хода одержать победу.

Это очень сложная головоломка, в которую следует играть вдвоем. При этом соперники должны обладать математическими способностями и определенными знаниями.

Условие

Один из игроков задумывает 10 натуральных чисел: s1, s2, s3, ..., s10. Соперник старается угадать их, задавая определенные вопросы. Разрешается задавать вопросы следующего типа: чему равна сумма b1s1 + b2s2 + ... + b10s10, где b1, b2, ..., b10 – некоторые натуральные числа?

При этом угадать задуманные числа следует не более, чем за 5 вопросов.

Подсказка: первым вопросом следует узнать, что все числа s1, s2, s3, ..., s10 меньше некоторой константы.

Решение

Выяснить, какие числа загадал соперник, вы можете всего за два вопроса. За первый вопрос следует узнать значение выражения s1 + s2 + s3 + ... + s10.

Предположим, что оно равно m. Возьмем достаточно большое число n, такое, что 10n > m. Задав второй вопрос, нужно узнать значение выражения s1 + 10ns2 + 102ns3 + ... + 109ns10.

Если значение этого выражения равно r, то в десятичной записи числа r справа налево будут идти группы из n-цифр, дающие десятичные записи чисел s1, s2, s3, ..., s10, возможно с несколькими нулями впереди (поскольку s1, s2, s3, ..., s10 < 10n, при сложении чисел s1, 10ns2, 102ns3, ..., 109ns10 в столбик переносов не возникает).

В эту игру следует играть вдвоем. Как и в предыдущей игре, соперникам нужны определенные знания математики.

Условие

Игроки по очереди вычеркивают 9 чисел (по своему выбору) из последовательности 1, 2, ...,100, 101. После одиннадцати таких вычеркиваний останутся 2 числа. Первому игроку присуждается столько очков, какова разница между этими оставшимися числами.

Подсказка: первым ходом нужно вычеркнуть числа из середины.

Решение

Первым ходом вам следует вычеркнуть 9 чисел от 47 до 55. Остальные числа разбиваются на пары: 1 – 56, 2 – 57, ..., 46 – 101. После каждого хода соперника вам нужно вычеркнуть числа таким образом, чтобы в каждой паре было вычеркнуто или оба числа, или ни одного.

Таким образом, в конце останется пара чисел, разность которых равна 55. Это самое большое количество очков, которое можно получить в этой игре.

Криптарифм – это математический ребус, в котором зашифрован пример на выполнение одного из арифметических действий. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Считается, что никакое число не должно начинаться с нуля.

Замените звездочки цифрами от 1 до 9. Каждая цифра используется только один раз.

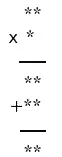
Ответ