Александр Волков - Артиллерия

Как раз в это время появилась новая цель: один из разведчиков доложил, что он видит дымки от выстрелов минометной батареи, открывшей огонь из кустов, влево от придорожной горки.

Быстро проверил командир батареи доклад разведчика: пригнулся сам к стереотрубе и тотчас увидел цель.

Вот она: от придорожной горки влево 40–маленькие кустики" метров на 500 подальше этой горки. Четыре легкие струйки сизого дыма дрожат на опушке кустиков, и вслед за этим слышится с той стороны свист приближающихся мин.

Это – действительно минометная батарея противника. Так как наша батарея не была занята стрельбой по другим целям, то командир батареи тут же решил подавить эту цель, потому что минометный огонь противника задерживал нашу пехоту и наносил ей потери.

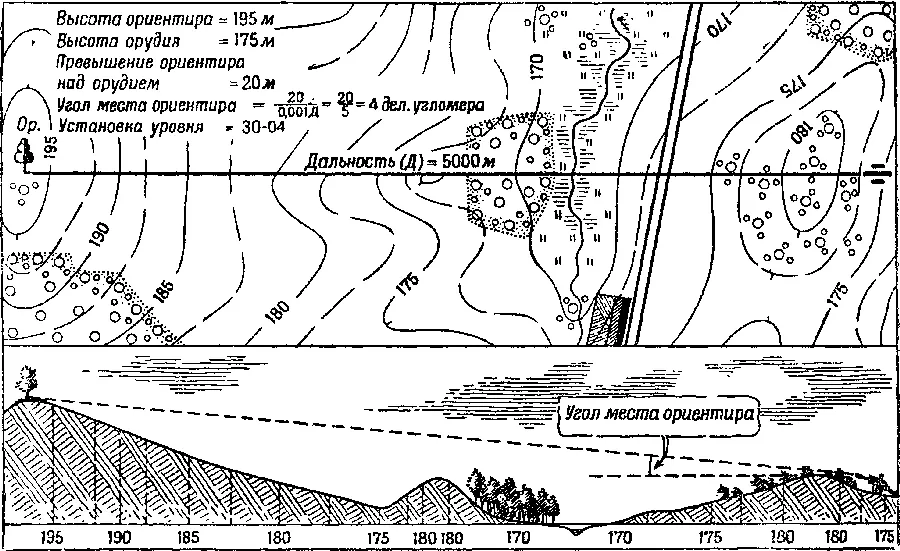
Рис. 299. Так подсчитывают по карте исходную установку уровня

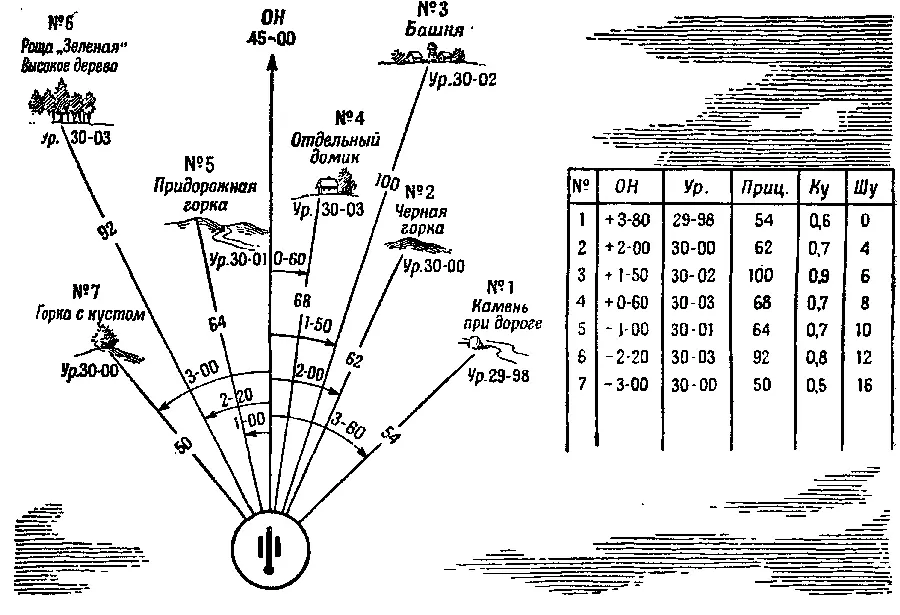
Рис. 300, Так можно вычертить схему переносов огня

Взгляд на карту, чтобы проверить удаление кустиков от придорожной горки, и одновременно – команды:

"По минометной батарее. Гранатой. Взрыватель осколочный. Заряд шестой".

Быстро мелькает ряд чисел в уме командира батареи, – и расчеты готовы. Он командует:

"Основное направление, левее 1–30. Уровень 30–01. Прицел 74. Первому один снаряд. Огонь!"

Подготовленная схема помогла быстро направить огонь батареи на новую цель. Можно было воспользоваться также результатами первой проведенной стрельбы: это тоже помогло бы быстро и достаточно точно перенести огонь на новую цель.

Теперь, когда исходные данные подготовлены по карте, даже первые снаряды сразу ложатся близко к цели: первый же разрыв оказывается против левого края цели; виден недолет.

Ошибки определения дальности при работе по карте не так велики, как при работе на глаз: ошибка составляет в среднем всего лишь 4 процента дальности. Первый окачок пределом достаточно сделать в 4 деления – так учат "Правила стрельбы".

"Левее 0–08. Прицел 78. Огонь!" – прозвучала команда.

Вы, конечно, не ожидали, что после полученного недолета командир батареи скомандует: "Левее 0–08". Зачем нужно менять направление стрельбы, если на прицеле 74 бокового отклонения разрыва не было?

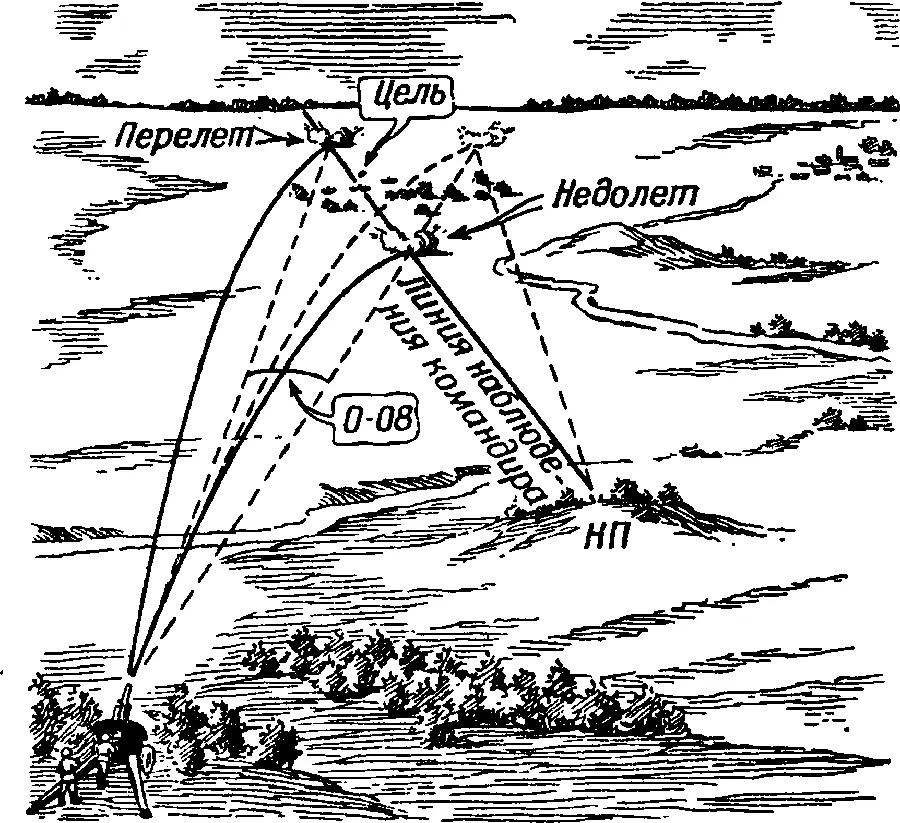
Рис. 301, При увеличении прицела надо менять направление стрельбы, иначе разрыв уйдет с линии наблюдения

Посмотрите на рис. 301 и вы поймете, что командир батареи поступил правильно.

Что получилось бы, если бы при увеличении прицела на 4 деления командир батареи не скомандовал "Левее 0–08" и орудие выстрелило в прежнем направлении?

Разрыв отклонился бы вправо от линии наблюдения командира. Дело в том, что командир батареи находится не только впереди огневой позиции, но и в стороне от нее...

Но вот снова прозвучал выстрел, снова зашуршала в воздухе граната... Перелет!

На прицеле 76 в батарейной очереди получились уже перелеты и недолеты. Это значит, что средняя точка падений недалеко от цели.

"Два снаряда, беглый огонь!"

В следующие 3–4 минуты минометная батарея противника была подавлена и прекратила огонь.

Вы убедились в том, что артиллеристу на поле боя приходится решать ряд математических задач. Вероятно, эти задачи показались вам очень простыми, и вам кажется странным, почему в артиллерии придают такое большое значение математике, почему принято говорить, что хорошими офицерами–артиллеристами могут стать только хорошие математики.

Не удивляйтесь – до сих пор мы выбирали для примеров только простейшие случаи, умышленно не затрудняли вас расчетами и вычислениями, чтобы понятнее была суть описанных приемов стрельбы,

Но если вас интересует "артиллерийская математика", посмотрите, как выполняются расчеты и как решаются некоторые артиллерийские задачи.

Вы познакомились уже с тем, как командир батареи вычисляет коэфициент удаления. Рассмотрим подробнее, как решает он эту задачу. Для этого ему надо знать всего лишь два расстояния: командир – цель (его обозначают сокращенно буквами Дк – дальность от командира до цели) и батарея – цель (Дб – дальность от батареи до цели).

Отношение Дк/Дб называют коэфициентом удаления, обозначая его буквами Ку. Таким образом, первая формула, которой пользуется каждый артиллерист, имеет следующий вид:

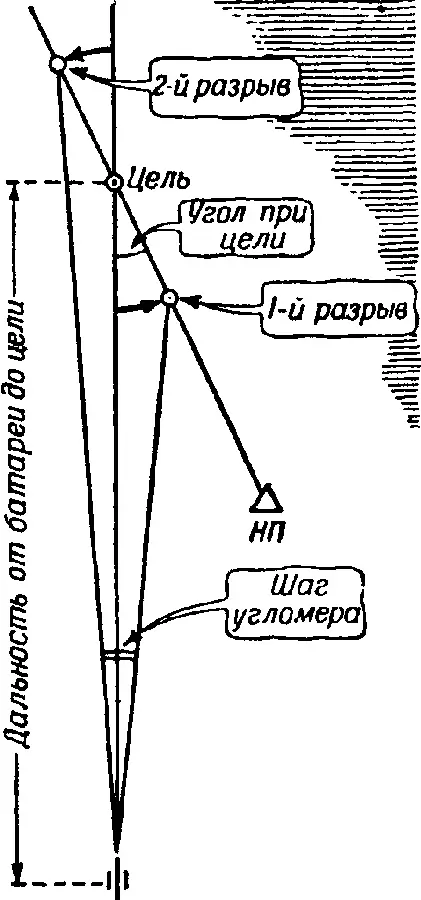
Рис. 302. Шаг угломера

Вы уже видели на примере первой пристрелки, что применение этой формулы помогает правильно решить задачу.

Коэфициент удаления избавляет от лишних расчетов, помогает артиллеристам экономить снаряды и время. Но коэфициент удаления можно применять, когда командир не очень далеко ушел в сторону от батареи (угол при цели не более 5–00).

Когда командир находится в стороне от батареи, разрывы сойдут с его линии наблюдения при изменении установки прицела. Их надо удерживать на линии наблюдения, исправляя направление одновременно с изменением установки прицела.

Поправка направления, при помощи которой при изменении установки прицела удерживают разрыв на линии наблюдения, называется шагом угломера (рис. 302).

Этот шаг угломера можно тоже заранее рассчитать по формуле, известной каждому артиллеристу: угол при цели или так называемую поправку на смещение (ПС) надо разделить на количество сотен метров, которое содержится в расстоянии от батареи до цели, и тогда получится шаг угломера:

Шу=ПС/0,01 Дб

Проще всего вычислить шаг угломера, когда мы готовим данные по карте: угол при цели нетрудно измерить при помощи целлулоидного круга.

И в других случаях нам тоже поможет математика. Мы можем, например, заменить карту несложным чертежом, который даст ответ на интересующий нас вопрос.

Кстати, этот же чертеж поможет нам сделать первый выстрел не наугад.

Возьмите листок бумаги и поставьте где угодно точку – это ваш наблюдательный пункт, или, сокращенно, НП (рис. 303). Проведите прямую линию вверх. На ней отложите в масштабе, которым вы задались (например, в одном сантиметре 200 метров), расстояние до цели, положим, 2000 метров. Здесь на чертеже окажется цель. Теперь подойдите к буссоли и направьте ее нолем в цель.

Но цель находится далеко и видна плохо. На помощь вам приходит монокуляр буссоли с шестикратным увеличением: оптическая ось монокуляра направлена всегда параллельно диаметру 30 – 0 буссоли (см. рис. 283).