David Laserna - Гюйгенс Волновая теория света. В погоне за лучом

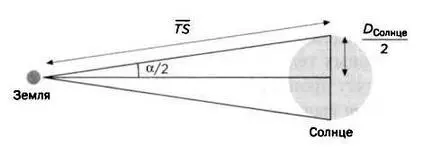
Введя значение α = 30'30": TS = 113 · D Солнцеи апеллируя к небесной гармонии, Гюйгенсу удалось установить, что D Солнце= 111 · D Земля. Поэтому:

TS =113 · D Солнце= 113 · 111 · D Земля= 12543 · D Земля,

Поскольку радиус Земли был определен достаточно точно, последнее уравнение дает нам искомый параметр масштаба для создания карты Солнечной системы Кеплера и Коперника — расстояние между Солнцем и Землей.

D Вен= 1/84 D Солнце· D Марс= 1/166 D Солнце· Среднее(1/84+1/166)/2 ≈ 1/111 D Солнце.

Следовательно, D Земля= 1/111 D Солнце.

Стремясь сохранить гармонию всей системы, Гюйгенс отклонялся от научной строгости и все больше уходил в область неясных гипотез. Ученый сам признавал, что его доводы с определенного момента опирались на весьма «шаткое основание». Он определил, что диаметр Солнца в 111 раз больше диаметра Земли. И это был прекрасный результат, учитывая, что, согласно современным расчетам, верное число равно 109. Во времена Гюйгенса уже можно было более или менее приемлемо измерить диаметр Земли. Полученное значение позволило ученому перевести все расстояния и размеры из относительных величин в абсолютные и определить масштаб Солнечной системы. Надо сказать, что с расчетами ученому помогла и фортуна: некоторые его ошибки уравновесили друг друга и, таким образом, исчезли. Хроматическая аберрация размывает очертания небесных тел, увеличивая их угловой диаметр. Это увеличение компенсируется тем, что Земле были приписаны меньшие размеры по сравнению с истинными, так как на самом деле она больше Марса и Венеры. В любом случае, точность полученного результата не может не поражать.

Как и другие отцы-основатели современной науки, Гюйгенс имел свою навязчивую идею родом из Средневековья. Кеплер представлял Солнечную систему в виде своеобразной матрешки, состоящей из геометрических фигур, а орбиты планет последовательно помещались в сферу или одно из пяти Платоновых тел. Ньютон обдумывал такую странную задачу, как расчет пропорций храма Соломона. Гюйгенс же в Systema Satumium выводит нумерологическую зависимость на основе числа 6, учитывая, что 6 = 3 х 2 х 1; 6 = 3 + 2 + 1. Ученый предсказывал, что больше не будет открыто ни одного спутника, поскольку их число должно быть таким же совершенным, как и число их старших братьев, планет. Известных планет было шесть, значит, и спутников должно быть шесть. У Земли свой спутник был, у Юпитера, как открыл Галилей, их было четыре, Гюйгенс закрыл этот список, разглядев Титан. Однако позже Кассини нарушил эту гармонию чисел, найдя на небе еще один спутник, опять же у Сатурна, — Япет.

Главным возражением против теории твердого диска, которую защищал Гюйгенс, является его стабильность. Сила притяжения уменьшается обратно пропорционально квадрату расстояния между массами (коэффициент пропорциональности — 1 /r 2, где r — расстояние). Представим себе планету Р, перед которой выстроились две одинаковые сферы, а и b отделенные друг от друга некоторым расстоянием (см. рисунок 5). В этом случае r 2будет больше, чем r 1поэтому притяжение между Р и а будет больше, чем между Р и b и обе массы будут иметь тенденцию отдаляться друг от друга.

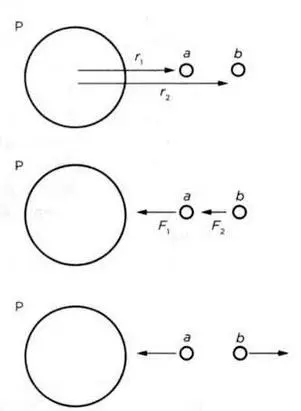
РИС. 5

РИС. 6

Если бы эти две сферы были частью массы единого тела, асимметрия воздействия деформировала бы его. К тому же из- за обратной зависимости силы притяжения от квадрата расстояния (1 /r 2) разница напряжения растет по мере приближения любого тела к планете. Интенсивность воздействия особенно чувствительна к изменениям расстояния при небольших значениях r, как видно на рисунке 6.

На кривой лежат значения 1 /r 2. Слева, рядом с началом координат, значения коэффициента больше и они сильно отличаются между соседними точками. Между конечными точками сферы а 1/r 2переходит от 4 к 1. Разница составляет целых 3 единицы. Справа, далеко от начала координат, коэффициент принимает меньшие значения. Между конечными точками b, которые находятся на одинаковом расстоянии от концов я, 1 /r 2переходит от значения 0,0178 к 0,0156. В этом случае разница не больше 0,0022 единицы.

Таким образом, даже если бы а и b были одинакового размера, на их крайние точки воздействовали бы силы разной интенсивности: в левой части графика, при меньшем г (когда сфера находится очень близко от планеты), эти силы были бы значительны и еле заметны — в правой части (когда сфера далеко). Следовательно, сфера едва почувствует присутствие Р, пока будет далеко, и будет испытывать разрушительное напряжение, если подойдет слишком близко. Мы можем рассмотреть этот процесс последовательно, по мере того как эластичная сфера приближается к планете Р. При этом она будет испытывать все большее воздействие. Сначала сфера превратится в яйцо, которое постепенно будет сплющиваться, становиться все более плоским, пока центростремительные силы не будут нивелированы, и сфера не разрушится.

Расстояние, на котором происходит разрушение тела из-за воздействия на него разнонаправленных сил притяжения, называется пределом Роша. Основное сопротивление деформации оказывают электромагнитные силы, которые притягивают друг к другу частицы, составляющие массу тела (химическое взаимодействие). Их работа тем эффективнее, чем меньший объем имеет тело. Таким образом, космонавт или коммуникационные спутники, вращающиеся вокруг Земли, находятся внутри предела Роша, но благодаря своим маленьким размерам защищены от разрушения. Сила притяжения возводит вокруг планет барьер, который разрушает тела определенного размера в непосредственной близости от них. Радиус орбиты больших спутников, таких как Луна, всегда превосходит предел Роша. Среди всех планет Солнечной системы звание главного разрушителя получил Юпитер — все кометы, подошедшие к планете слишком близко, исчезли.

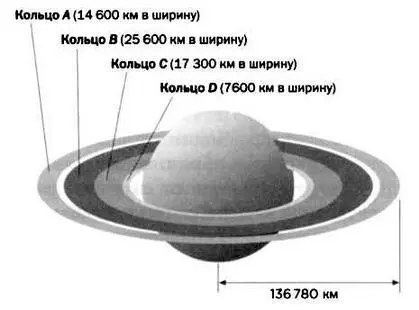
РИС. 7

Если силы притяжения особенно велики, деформации подвергнутся и мелкие тела. Черная дыра может вызвать настолько неравное напряжение между ногами и головой человека, что способна убить его (это явление неформально называется «спагеттификацией»).

Кольца Сатурна состоят из множества кусочков льда и пыли, которые вращаются вокруг планеты на разных скоростях, очерчивая тысячи окружностей. Из-за гравитационного притяжения больших спутников на кольцах возникают трещины и щели, из-за чего они похожи на старую музыкальную пластинку. Буквами А, В, С и D (см. рисунок 7) обозначены четыре основные полосы, видимые с Земли. Алфавитный порядок отражает хронологию их открытия, а также их расположение — от внешнего края к внутреннему.