Григорий Ревзин - Николай Коперник

Коперник предвидит множество возражений. Но он уверен в своей правоте:

«Все это покажется неудобопонятным и даже невероятным. Но с божьей помощью мы докажем это яснее солнца, — по крайней мере, для знакомых с математикой».

Содержание последующих глав и книг «Обращений», в которых Коперник «с божьей помощью» подробно излагает свою гелиоцентрическую систему, опровергающую священное писание, касается уж деталей возведенного им здания. Все предпосылки от философии и мировоззрения заключены в первых десяти главах.

Коперник иногда ссылается на божественное провидение, однако учение его в своей основе, антирелигиозно.

Насколько Коперник был далек от всяких религиозных помыслов, творя свое новое мироздание, можно судить хотя бы по истинно языческому гимну Солнцу, который он включил в конец десятой главы. Церковные начетчики средневековья во все поры их христианской вселенной помещали господа-бога и его ангелов и святых. Человек Возрождения Николай Коперник видит мир совсем иными очами.

«В середине всех этих орбит находится Солнце! Ибо может ли прекрасный этот светоч быть помещен в столь великолепной храмине в другом, лучшем месте, откуда он мог бы все освещать собою? Поэтому не напрасно называли Солнце Душою вселенной, а ныне — Управителем мира. Трисмегист называет его Видимым богом, а Электра Софокла — Всевидящим.

И, таким образом, Солнце, как бы восседая на царском престоле, управляет вращающимся около него семейством светил. Земля пользуется услугами Луны, и, как выражается Аристотель в трактате своем «О животных», Земля имеет наибольшее сродство с Луною. А в то же время Земля оплодотворяется Солнцем и носит в себе плод в течение целого года».

Ни в «Малом Комментарии», ни в «Обращениях небесных сфер» великий ученый не оставил рассказа о том, как возникала и формировалась в его сознании идея гелиоцентрической системы мира.

Только дав волю своему воображению, можно представить себе ныне, через какие искания и сомнения должна была пройти мысль гения.

Прослеживая путь Коперника к коперниканству, приходится воссоздавать недостающие звенья при помощи более или менее удачных догадок и допущений.

Современные исследователи с большой степенью убедительности разрешили эту задачу при помощи несложного геометрического построения [158] Пользуемся построением профессора Н. Идельсона, данным им в статье «Николай Коперник» («Вестник знания». 1941, № 3). .

Астрономические таблицы древних дают следующие периоды обращений трех внешних планет — Марса, Юпитера и Сатурна:

По этим величинам можно рассчитать угловую скорость движения планет (иначе говоря, угол их смещения в единицу времени) в Птолемеевой системе. Для этого достаточно 360° разделить на число дней, в течение которых протекают эти обращения:

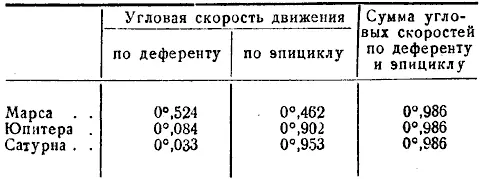
В этой таблице обращает на себя внимание равенство сумм угловых скоростей каждой из трех планет — 0°,986. Эта постоянная величина любопытна тем, что такой угловой скорости соответствует период обращения в 365 дней, иначе говоря — период видимого обращения Солнца вокруг Земли (360:0,986=365).

Таким образом, периоды обращения трех внешних планет как бы объединены между собой через период обращения Солнца.

Несомненно, что астрономы древности, оперируя со своими таблицами периодов обращений и угловых скоростей, наталкивались на эту постоянную величину. Несомненно также, что она должна была наводить их на мысль о какой-то связи, существующей в их геоцентрической системе между орбитой Солнца «и орбитами каждой из остальных планет.

Основные Птолемеевы точки — центр Земли — 3, центр эпицикла на деференте — О и планета (в данном случае Юпитер) — Ю — могут быть изображены так.

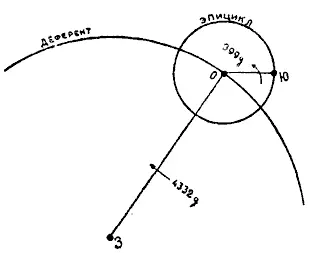
Введение в эту Птолемееву систему четвертой точки — С, помещенной так, что она вместе с тремя прежними точками 3, О и Ю составила параллелограмм, вносит две новые прямые — СЗ и СЮ, изображенные на чертеже.

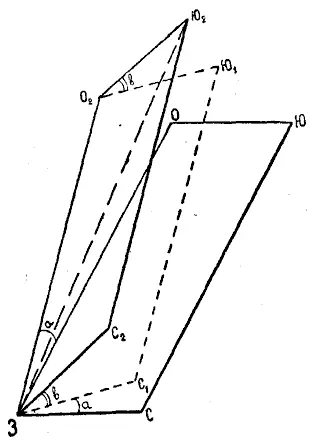
Поставленные в вершины параллелограмма шарниры позволяют вращать эту усложненную Птолемееву систему вокруг точки 3, где шарнир сделан неподвижным относительно плоскости чертежа. Если вращение производить со скоростями, указанными в таблице, то-есть чтобы линия 30 делала оборот вокруг неподвижной точки в 4332 дня (при угловой скорости 0°,084), с тем, что линия ОЮ оборачивалась бы вокруг точки О в 399 дней (при угловой скорости 0°,902), то линия ЗС сделает оборот вокруг неподвижной точки 3 в 365 дней. Это нетрудно доказать.

Предположим, что прямая ЗО за день отошла бы от своего исходного положения на угол а без смещения точки Ю (Ю 1) относительно точки О (O 2), то-есть без изменения углов параллелограмма, который в этом случае занял бы положение 3O 2Ю 1С 1. Тогда прямая ЗС отошла бы от своего исходного положения тоже на угол а. Но так как за то же время точка Ю сместится относительно точки О, то-есть прямая ОЮ повернется в отношении к ее исходному положению ОЮ (или O 2Ю 1) на угол в, так что параллелограмм займет положение ЗO 2Ю 2С 2, то прямая ЗС повернется при этом еще и на угол в. Таким образом, прямая ЗС за день отойдет от своего исходного положения на угол а+в. следовательно, ее угловая скорость будет равна сумме обеих заданных угловых скоростей (0°,084 + +0°,902 = 0°,986 в день).

Итак, период обращения точки С вокруг неподвижной точки 3 равен 365 дням, и, очевидно-, точку С можно принять в схеме Птолемея за Солнце. Птолемеева прямая ОЮ, всегда равная и параллельная ЗС, является, следовательно, отображением орбиты Солнца относительно Земли. А диагональ переменной длины ЗЮ 2отображает движение Юпитера также относительно Земли.

Придя к этому важному выводу, мы наталкиваемся, однако, на следующую трудность: Птолемеевы эпициклы Марса, Юпитера и Сатурна имеют радиусы различной величины. Вследствие этого и орбита Солнца в каждом из трех случаев не одинакова.

Можно ли устранить эту трудность и добиться единства всего построения? Это, оказывается, возможно. Дальнейшее преобразование построения и выражает сущность перехода от схемы Птолемея к идее Коперника!

Снимается точка О, центр Птолемеева эпицикла. Вместе с нею снимется радиус эпицикла ОЮ, а также сторона 30. От параллелограмма останутся только стороны ЗС и СЮ.