Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

Проведенный А. А. Власовым анализ дисперсионного уравнения для малых продольных колебаний изотропной электронной плазмы с максвелловской равновесной функцией распределения по скоростям показал, что в пренебрежении парными столкновениями частиц в области фазовых скоростей, превышающих тепловую скорость электронов, такие колебания не затухают и обладают следующим законом дисперсии:

где и ω p — известная со времен И. Ленгмюра плазменная (электронная ленгмюровская) частота, а 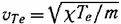— тепловая скорость электронов. Наличие спектра высокочастотных электронных колебаний с малой групповой скоростью

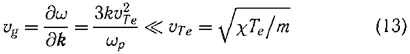
хорошо согласовывалось с известными экспериментальными результатами И. Легмюра и Л. Тонкса [8]. Подтверждением правильности теории А. А. Власова следует считать также то, что медленные продольные колебания в чисто электронной плазме оказались невозможными. Именно, в области v φ = ω/k << v Te поле таких колебаний экранируется, причем размер экранировки определяется дебаевским радиусом, что согласуется с глубиной дебаевской экранировки поля статического заряда в плазме (7), полученной Л. Д. Ландау из чисто термодинамических соображений [52] Следует отметить, что в цитируемой работе И. Легмюра и Л. Тонкса в рамках гидродинамического описания была развита идеология самосогласованного поля и, более того, получены спектры (12) (с небольшой неточностью: вместо коэффициента 3 в поправочном слагаемом они получили множитель 1) и дебаевская экранировка низкочастотного продольного поля. Ими же было показано, что малые возмущения в плазме не апериодически затухают со временем, а колеблются с частотой ω p и лишь слабо затухают вследствие столкновений электронов. .

Вместе с тем вызывало некоторую неудовлетворенность отсутствие затухания колебаний, хотя в приближении самосогласованного поля взаимодействие частиц учитывалось. Сам А. А. Власов в этом ничего плохого не видел. Более того, парную столкновительную релаксацию, которая, согласно теории Л. Д. Ландау, определяется частотой электрон-ионных столкновений

он считал пренебрежимо малой, поскольку

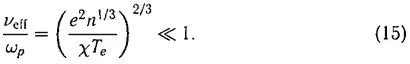
Более существенным А. А. Власову представлялось дисперсионное расплывание. Оценивая исходя из формулы (12) время расплывания τ g неоднородности с размером 1/ k , находим, что

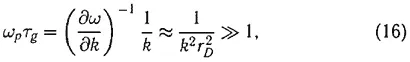
т. е. это время велико по сравнению с периодом колебаний. Причем роль столкновений определяется величиной ν eff τ g , которая есть произведение малого параметра (15) на большой параметр (16).

4. В [2] Л. Д. Ландау резко отрицательно отреагировал на отсутствие в теории А. А. Власова диссипации малых колебаний при пренебрежении парными столкновениями. Считая уравнение Власова применимым для описания электронных колебаний плазмы, он тем не менее писал: «Власов искал решения вида exp( —iωt + i kr ) и определял зависимость частоты ω от волнового вектора k . В действительности вообще не существует никакой определенной зависимости ω от k , и при заданном значении k возможны произвольные ω ». Решая, как и А. А. Власов, начальную задачу для малых колебаний, Л. Д. Ландау приходит к тому же дисперсионному уравнению [53] Ландау вообще не воспринимал введение дисперсионного уравнения, что особенно резко прозвучало в статье [5].

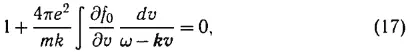
которое исследовалось А. А. Власовым. Здесь f 0( v ) — равновесная функция распределения по скоростям, которая считается максвелловской и нормированной на плотность электронов n :

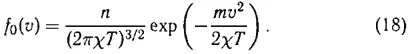
В уравнении (17) фигурирует несобственный интеграл Коши с полюсом подынтегрального выражения на действительной оси интегрирования при v = ω/k . Именно в понимании этого интеграла и возникло разночтение между А. А. Власовым и Л. Д. Ландау. А. А. Власов считал, что интеграл надо брать в смысле главного значения, и как результат получил решение уравнения (16) в виде незатухающих колебаний со спектром (12). Л. Д. Ландау же указал, что интеграл надо брать по контуру (правило обхода Ландау), соответствующему представлению полюса в виде

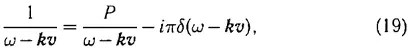
где P означает интеграл в смысле главного значения. Это приводит к появлению у частоты малой мнимой поправки ( ω → ω + γ )

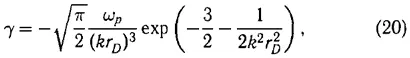
описывающей слабое затухание колебаний со спектром (12). Это затухание и стало впоследствии именоваться как «бесстолкновительное» затухание Ландау. Слово «бесстолкновительное» мы поместили в кавычки, поскольку в действительности уравнение Власова многочастичные (или коллективные) столкновения частиц учитывает; оно не учитывает лишь ближние парные взаимодействия. Для учета парных взаимодействий, как мы уже знаем, надо дополнить уравнение Власова в правой его части интегралом столкновений. Учет парных столкновений приведет к дополнительному затуханию δγ , причем

где ν effдается выражением (14).

Столкновительное затухание (21), так же как и «бесстолкновительное» (20), является малым по сравнению с частотой колебаний (12), что обеспечивается неравенствами (15) и (16). Однако возникает вопрос о соотношении между ними, или, другими словами, о соотношении между столкновительным затуханием и «бесстолкновительным» затуханием Ландау. При условии