Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

1. 1996-й год является юбилейным: на него приходится ряд дат, которые связаны с некоторыми вехами в развитии кинетической теории плазмы как газа системы частиц с электромагнитным взаимодействием. Шестьдесят лет назад, т. е. в 1936 г., была опубликована одна из наиболее цитируемых работ Л. Д. Ландау «Кинетическое уравнение в случае кулоновского взаимодействия» [1], в которой был получен знаменитый интеграл упругих кулоновских столкновений заряженных частиц — интеграл Ландау, играющий важную роль в кинетической теории плазмы. Десять лет спустя, в 1946 г., появилась не менее популярная работа Л. Д. Ландау «О колебаниях электронной плазмы» [2], в которой исходя из кинетического уравнения Власова было открыто новое явление — «бесстолкновительное» затухание электронных ленгмюровских колебаний, получившее название затухания Ландау. А в промежутке между этими статьями Л. Д. Ландау в 1938 г. была опубликована основополагающая работа А. А. Власова «О вибрационных свойствах электронного газа» [3], в которой было получено кинетическое уравнение для плазмы в первом основном приближении по кулоновскому взаимодействию — приближении взаимодействия через самосогласованное поле. Это уравнение получило название уравнения Власова. Хотя в то время оно было недостаточно строго обосновано, но именно полученные с помощью этого уравнения, в том числе в первую очередь самим А. А. Власовым, результаты составили основу современной кинетической теории плазмы. Строгое обоснование уравнения Власова было дано в 1946 г. в монографии Н. Н. Боголюбова «Проблемы динамической теории в статистической физике» [4]. В 1996 г. исполняется 50 лет и этой прекрасной книге, в которой Н. Н. Боголюбовым было обосновано не только уравнение Власова как основное приближение для газа кулоновски взаимодействующих частиц, но также показано, что интеграл столкновений Ландау учитывает следующий порядок по кулоновскому взаимодействию частиц в плазме. Уравнение Власова, дополненное интегралом столкновений Ландау, образует общее кинетическое уравнение для плазмы, которое следовало бы назвать уравнением Власова-Ландау. Таким образом, творцами кинетической теории плазмы следует считать А. А. Власова и Л. Д. Ландау. Ниже мы кратко обсудим работы Л. Д. Ландау [1, 2] и А. А. Власова [3] с позиции сегодняшнего дня (которая, по существу, совпадает с позицией, предложенной в монографии Н. Н. Боголюбова [4]). В заключение же, подводя итог, дадим свою оценку (и только оценку) критической статье четырех авторов [5] и ответу А. А. Власова, который, к сожалению, был опубликован в малоизвестном в то время ведомственном журнале [6].

2. К началу 1930-х годов возникла острая необходимость в построении кинетической теории плазмы как нейтрального в целом газа заряженных частиц: электронов и ионов. Она диктовалась в первую очередь экспериментальными работами И. Ленгмюра, исследовавшего релаксационные процессы в плазме газового разряда в широком диапазоне плотностей и температур частиц. Первым, кто достиг существенного прогресса на этом пути, был Л. Д. Ландау, который в 1936 г. получил кинетическое уравнение для газа с кулоновским взаимодействием частиц. При выводе кинетического уравнения для функции распределения f ( p, r, t ) определяющей вероятность обнаружения частицы с импульсом p в точке r в момент времени t , Ландау исходил из уравнения Больцмана, в котором изменение f( p, r, t) определяется парными столкновениями [49] Как и в работах Л. Д. Ландау и А. А. Власова, ограничиваемся рассмотрением только электронной плазмы, считая ионы бесконечно тяжелыми.

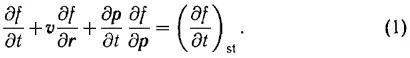
Здесь

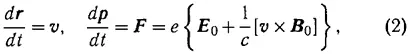
а ( df/dt ) st — интеграл парных упругих столкновений, являющийся билинейным функционалом f ( p, r, t ). В соответствии с духом больцмановского приближения сила F может быть только внешней, так что и поля E 0и B 0могут быть только внешними, их источниками в уравнениях Максвелла являются заданные плотности заряда ρ 0и тока j 0.

Здесь уместно заметить, что при написании уравнения (1) для обычного газа незаряженных частиц Больцман рассматривал частицы как твердые сферы с геометрическим радиусом a 0(радиусом взаимодействия). Условие применимости кинетического описания посредством уравнения (1) для такой системы записывается в виде

где n 0— плотность частиц. Это неравенство, соответствующее малости размера частиц a 0, т. е. радиуса их взаимодействия, по сравнению со средним расстоянием между частицами есть условие применимости газового приближения для системы нейтральных частиц. Оно означает, что частицы основное время находятся в свободном полете и лишь изредка сталкиваются. При этом, хотя потенциал взаимодействия и бесконечно велик, т. е. взаимодействие сильное, происходит такое взаимодействие редко.

Л. Д. Ландау при выводе уравнения (1) для газа из кулоновски взаимодействующих частиц условием типа (3) воспользоваться не мог, поскольку характерный радиус взаимодействия в этом случае «бесконечно» велик. Он воспользовался малостью средней потенциальной энергии взаимодействия частиц e 2n 1/3 по сравнению со средней кинетической энергией теплового движения χT и за условие газовости плазмы принял

где e — заряд электрона, n — плотность электронов, а χ — постоянная Больцмана. Это позволило ему получить сходящийся интеграл парных столкновений и записать кинетическое уравнение (1) в виде

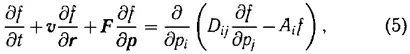
где

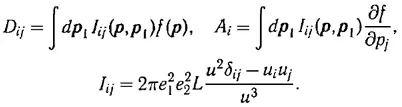
Здесь u = v — v 1 — относительная скорость сталкивающихся частиц, а L — кулоновский логарифм

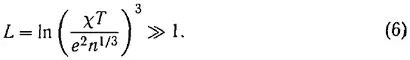
Суммирование в (5) распространяется по электронам и ионам.

Заметим, что при условии (4) поле пробного статического заряда q в плазме оказывается экранированным, причем потенциал поля дается формулой