Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

«Парадокс» разъясняется тем, что формулы (15) и (15а) обе законны, но относятся к разным физическим случаям. Именно, формула (15а) предполагает закрепление граничных атомов цепочки, для которой она выведена. Формула же (15) свободна от указанной предпосылки. Поэтому и не удивительно, что они приводят к различным результатам.

Факт реализации «закреплений», которыми работают «обычные» методы, в действительности принципиален.

Обычные методы статистической механики допускают как само собой разумеющийся факт возможность произвольной пространственной локализации отдельных частиц ансамбля. Это обстоятельство выступает, например, в некоторых краевых задачах, в которых используются операции «закрепления» отдельных атомов (в цепочке, например, двух крайних).

Однако обычные экспериментальные средства, при помощи которых изучают совокупность частиц, не гарантируют подобной локализации. Этому обстоятельству имеется соответствие в математическом аппарате. Оно состоит в том, что метод «самосогласованного поля» запрещает такую локализацию.

Такова особенность тех решений проблемы многих тел, которые данный метод представляет. Этот метод соответствует другим граничным условиям, налагаемым на функцию распределения D чем принципиально физически и математически отличается от «обычных» методов.

Для ансамбля N одинаковых частиц функция распределения имеет вид

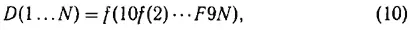
где f — одна и та же функция для всех частиц ансамбля, и, таким образом, невозможно, не выходя за рамки решений, предоставляемых методом «самосогласованного поля», задавать произвольно вид функции распределения для какой-либо одной частицы ансамбля независимо от остальных, а именно это и требуется для осуществления «закреплений» в «обычных» методах.

Таким образом, математический и физический смысл метода «самосогласованного поля» (для одинаковых частиц) запрещает локализацию отдельных частиц ансамбля.

Метод «самосогласованного поля» порочен, так как из исходной формулы видно, что характер решения может существенно зависеть от K' (0) или K'' (0), т. е. «распространение плотности существенно зависит от характера закона взаимодействия при бесконечно малом расстоянии между частицами, что нелепо уже само по себе» [К].

Могло бы казаться, что метод «самосогласованного поля» не корректен, так как из исходного уравнения (1) с самосогласованным потенциалом

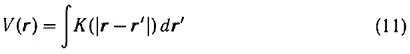
видно, что характер решения может существенно зависеть от K (0), т. е. распределение плотности («макро» характеристика) может существенно зависеть от характера закона взаимодействия при бесконечно малом расстоянии между двумя частицами («микро» характеристика), что кажется невероятным.

Но если бы эта зависимость была чувствительной, то непосредственная связь между «микро» и «макро» не являлась бы внутренним противоречивым дефектом теории, а отображала бы ее природу — таков характер теории (интегральные уравнения).

Действительное положение, однако, сложнее.

Ход «ядра» в нуле в уравнении с «самосогласованным» потенциалом (11) определяется расположением частиц не при непосредственном совпадении их центров, а в некоторой малой, но конечной окрестности, и, более того, величина этой области и ход «ядра» внутри этой области в свою очередь зависят от «макро» величин — от распределения плотности вероятности местоположения частиц.

В самом деле, запишем потенциал на основании формулы для ряда Тейлора-Вольтерра (1) так:

откуда видно, что ход ядра « K'' » вблизи нуля определяется всеми последующими членами ряда Тейлора. Физически это означает, что, например, на поведение двух частиц при их сближении оказывают влияние, и все большее с уменьшением их расстояния, не «парные» взаимодействия, а «коллективные» в смысле § 1, т. е., например, третья частица (входящая в состав «тройного» взаимодействия K 012 ) и т. д.

Таким образом, для точного уравнения (1) нет проблемы. Естественно, ее не должно быть и для приближенного уравнения, для которого «самосогласованный» потенциал взят просто в виде (11), если приближение взято правильно.

Приближенность соответствует предположению независимости ядра « K'' в (11) от p (линеаризация ядра), что возможно не только для достаточно больших расстояний, когда можно опустить последующие члены ряда Тейлора, ибо степень быстроты их убывания сильно возрастает с увеличением числа членов, но и для достаточно малых расстояний по сравнению и с периодом изменения p — и считать поэтому величину p постоянной.

Таким образом, нет оснований сомневаться в характере приближения.

Ядро приближенного уравнения с потенциалом (11) имеет вид вблизи нуля (полагаем ρ = ρ 0)

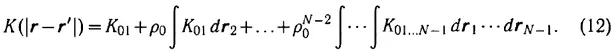
В итоге получается результат: Зависимость ядер интегрального уравнения с самосогласованным потенциалом (11) вблизи нуля, а следовательно, и решения уравнений существенно зависят от характера закона взаимодействия коллектива частиц (совокупность интегральных членов), в котором закон взаимодействия только двух частиц играет уже сравнительно малую роль.

[Пункты 4–6 опущены.]

Рассмотрением пяти возражений исчерпано содержание критики моих работ. Это рассмотрение показывает, что выдвинутые пять возражений против основ теории и ее следствий преждевременны, и, более того, анализ указывает на их ошибочность.

Именно:

Первое возражение: «Для короткодействующих сил основное уравнение неприменимо».

Это суждение дано критиками без доказательства. Рассмотрение, однако, показывает, что основное исходное уравнение теории, в сущности, не зависит от быстроты убывания сил взаимодействия с расстоянием между частицами, а определяется несколько другими критериями (см. § 1 и 2).

Второе возражение: «Метод “самосогласованного поля” находится в противоречии с обычными методами статистики».

Третье возражение: «Никакого дисперсионного уравнения не существует», так как, во-первых, допущена ошибка: нельзя делить на нуль, во-вторых, выбор «главного значения» произволен.

Дисперсионное уравнение существует и приводит к важным результатам (§ 5 и 6), однако представляет только частное, но наиболее важное решение исходного уравнения.