Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

Добавим еще, что если в (1) K ( r ) заменить на K ( r )exp( K ( r ) /kT ) (так пытается усовершенствовать свое уравнение А. А. Власов в конце работы [2]), то, хотя ход дискуссии изложенного нами вопроса и ее результаты и изменяется, но при этом возникнут новые трудности и новые противоречия с результатами классической статистики.

Исходя из разобранных выше посылок А. А. Власов приходит к ряду выводов, относящихся к теории кристаллического состояния. Один из этих выводов, касающийся «наличия кристаллической структуры и ее спонтанного возникновения» [1, § 10; 3, § 9] мы и разберем здесь, так как он приводит автора к далеко идущим утверждениям. Именно на основании этого вывода он говорит о «новой теории кристаллического состояния, совершенно отличной от теории М. Борна, в которой позиция каждого атома фиксирована около положения равновесия» [1, с. 40].

Решая уравнение, получающееся из (1) с помощью линеаризации, автор приходит к выводу, что у последнего при известных условиях имеются периодические решения. Эту периодичность, как это особенно четко сформулировано им в начале § 9 статьи [3], он истолковывает как наличие кристаллической структуры. Период ее определяется уравнением (УШ) работы [2], которое при использовании формулы (8) той же работы принимает вид

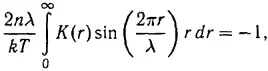
где λ — период структуры. Согласно этой формуле, период λ является функцией не только концентрации атомов N , но и температуры T . Однако это, очевидно, невозможно, поскольку среднее число частиц N в единице объема задано. Период простой решетки равен N - 1/3 (или при сложной структуре ячейки отличается от этой величины множителем) и явно от температуры все зависит.

Тот факт, что интерпретация решений уравнения (1) в этом случае приводит автора к таким странным следствиям, не должен нас удивлять, так как этот случай лежит вне границ физической применимости используемого уравнения.

2. Выше мы разбирали вопросы, связанные с теорией твердого тела. Помимо этого А. А. Власов в указанных работах (см. в особенности [1]) рассматривает нестационарные явления в многоатомных системах. Исходной здесь служит система уравнений (11) из работы [2], причем член дf/дt полагается равным нулю и проводится линеаризация, т. е. решение пишется в виде f = f 0+ ф , где ф<0. В результате получается следующее уравнение (3) в [3]):

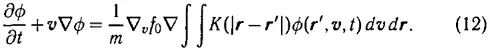
Автор ищет решение этого уравнения в виде

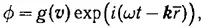
что в результате подстановки в (12) приводит к уравнению для g

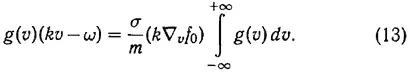
Далее А. А. Власов (см. (4) в [1]) делит обе части этого уравнения на ( kv — ω ), затем интегрирует обе части по dv и приходит таким образом к основному для него «дисперсионному уравнению» (см. (5) в [1])

Из этого уравнения автор считает возможным определить связь между k и ω . Нахождению этой связи в различных случаях и посвящена большая часть работы [1]. Между тем уравнение (14) бессмысленно, поскольку фигурирующий в нем интеграл расходится при kv — ω = 0.

А. А. Власов пытается обойти эту трудность просто тем, что берет главное значение интеграла, на что, разумеется, нет абсолютно никаких оснований, поскольку расходящийся интеграл можно «взять» также бесчисленным числом других способов. Как известно, если в физической проблеме встречается выражение, не имеющее математического смысла (например, расходящийся интеграл), то это означает, что либо в исходных уравнениях задачи не учтен какой-либо физический эффект, приводящий при его учете к разумным результатам, либо же при решении уравнений допущена математическая ошибка. В случае А. А. Власова дело обстоит именно последним образом, так как уравнение (14) вовсе не вытекает из интегрального уравнения (13). Из этого последнего уравнения вообще не получается какой-либо связи между ω и k таким образом, никакого «дисперсионного уравнения» не существует.

Ошибка А. А. Власова состоит в том, что, как мы указывали, он делит обе части (13) на kv — ω и, таким образом, принимает равенство (см. (4) в [1])

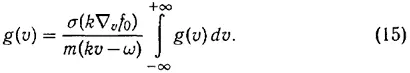
3. В действительности из (13) вытекает не (15), а уравнение, отличающееся от (10) добавленной к правой его части некоторой произвольной функцией от ω и v , равной нулю при к kv ≠ ω и отличной от нуля при kv = 0. Наличие содержащей известный произвол функции и должно обеспечить математическую непротиворечивость решения [46] Выражение (15) не вытекает из уравнения (13), так как решение этого уравнения должно быть интегрируемым, поскольку в (13) входит ʃ gv(dv) . Строго говоря, при ω ≠ 0 уравнение (13) в терминах обычного анализа, рассматривающего лишь функции в обычном смысле слова, вообще не имеет решения. Решение существует, если использовать «несобственные» функции типа δ(x) , что допустимо с точки зрения смысла задачи. . Для получения этого решения можно, например, применить к (13) преобразование Фурье. В результате для функции

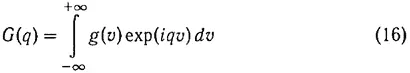
мы получаем

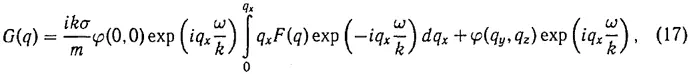
где

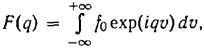
направление k принято за ось x и φ ( q y, q z ) — произвольная функция. Мы видим, что решение для G(q) содержит произвольную функцию φ ( q y, q z ) от двух аргументов. Такой же произвол содержится в сопряженной по Фурье с G(q) исходной функции g(v) (представляющей собой функцию несобственную). Кроме функции G ( q ) в (17) остаются произвольными все четыре параметра k x, k y, k z, ω, и никакой связи между ними не существует.

Кроме того, здесь нужно, конечно, иметь в виду все сказанное нами относительно неприменимости метода «самосогласованного поля». Тем не менее вопрос о дисперсионном уравнении заслуживает отдельного разбора, так как в работе 1938 г. [8] А. А. Власов применял уравнение (12) к электронной плазме. В этом же случае, поскольку рассматриваются кулоновские силы, применение самосогласованного поля и, следовательно, уравнения (eq12) допустимо. Однако исследование вопроса автор опять проводит на основе несуществующего «дисперсионного уравнения» (14), вследствие чего большинство результатов этой работы также неверно. Мы не будем останавливаться на этом вопросе, так как исследование колебаний электронной плазмы проведено в работе Л. Ландау «О колебаниях электронной плазмы» [6]. В этой работе указано, как нужно ставить вопрос о решениях уравнения (12), на чем останавливаться здесь мы также не будем.