Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

Таким образом, представления А. А. Власова (принимающего ведь классическую статистику) ведут к фундаментальному внутреннему противоречию. Кроме того, применение метода «самосогласованного поля» приводит (как мы также сейчас покажем) к результатам, физическая неправильность которых видна уже сама по себе.

Для случая термодинамического равновесия метод «самосогласованного поля» в том виде, в каком им пользуется А. А. Власов, сводится к следующему уравнению для плотности частиц (уравнение (26) из работы [2]):

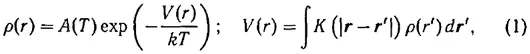
где K ( r ) — потенциал взаимодействия двух частиц.

К этому уравнению для определенности задачи должно быть, в сущности, добавлено еще условие нормировки ρ , задающее общее число частиц и состоящее в том, что это общее число частиц равно интегралу от ρ по всему объему, занятому телом. Из этого условия и должна быть определена зависящая от T постоянная A ( T ).

Рассмотрим решение уравнения (1) при очень низких температурах и сопоставим его с известными результатами классической статистики. Для простоты разберем одномерный случай, цепочку частиц, потенциал взаимодействия которых K ( x m- x n ) зависит только от расстояния между ними.

По классической статистике, применяя метод Гиббса, мы получаем следующее. Частицы находятся вблизи положений равновесий, определяемых из условий минимума потенциальной энергии системы

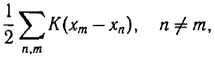
так как только при этом условии вероятность состояния имеет заметную величину. Условия равновесия для внутренних точек

удовлетворяется при периодическом расположении частиц: x n= nd , так как K' ( x ) — нечетная функция на x , и, следовательно:

период d зависит от величины внешней силы p (давления), действующей на поверхность тела:

Плотность частиц p(x) для ограниченной цепочки частиц, когда задача имеет определенное решение, равна

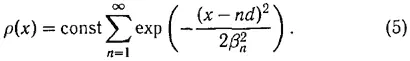
При этом средний квадрат β n 2 определяется известным путем, зависит от расстояния от конца цепочки и растет от края к середине ее (примерно по параболическому закону), как это и должно быть на основании простых и наглядных соображений.

Перейдем теперь к разбору свойств решений уравнения (1), применяемого А. А. Власовым при низких температурах. Уравнение это в одномерном случае сводится к такому:

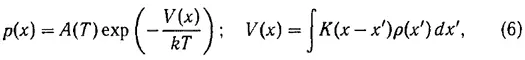
причем

где M — число частиц. Как видно отсюда, при T → 0 плотность ρ ( x ) будет иметь резкие максимумы и заметную величину вблизи точек x n , для которых V ( x ) имеет минимум и для которых, следовательно,

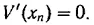
Для бесконечной цепочки точки x n будут расположены периодически, т. е. x n = nd .

Величину V ( x ) = ʃ K ( x — x' ) ρ ( x' ) dx' можно в этом случае, учитывая еще условие нормировки ρ ( x ), записать в виде суммы:

Теперь условие (7) дает

что совпадает с (3). Пока мы рассматриваем бесконечную цепочку, период остается неопределенным (мало того, в этом случае рассматриваемое решение заведомо не единственно; ρ ( x ) = const, очевидно, тоже удовлетворяет задаче). Для нахождения периода нужно и здесь рассмотреть ограниченную цепочку, при этом период будет определяться уравнением (4) и будет, таким образом, зависеть от внешней силы. На первый взгляд, на основании сказанного может показаться, что все обстоит благополучно и «теория самосогласованного поля» в рассматриваемом случае приводит в точности к тем же результатам, что и общие методы классической статистики. Дело, однако, обстоит не так. Действительно, найдем, например, выражение для плотности ρ ( x ). Для этого в (6) достаточно подставить V ( x ) из (8), разложив эту величину в ряд по степеням ( x — nd ) около каждого из узлов решетки. Этим путем найдем

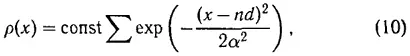
причем средний квадрат смещения частиц из положения равновесия равен

и одинаков для всех внутренних узлов цепочки. Из этой формулы, существенно отличающейся от выражения, вытекающего из классической статистики, виден также тот основной порок метода «самосогласованного поля», который и показывает его заведомую неприменимость к этим вопросам. Дело в том, что, как вытекает из вывода выражения (11), в сумме ∑ K ( nd ) присутствует член, соответствующий n = 0 .

Таким образом, формулы (10) и (11) показывают, что распределение плотности существенно зависит K'' (0) — от характера закона взаимодействия при бесконечно малом расстоянии между частицами, что нелепо само по себе. Заметим, что при нашем выводе мы молчаливо предполагали, что четная функция K(x) (где —∞ < x < +∞) непрерывна вместе со своими производными первого и второго порядка при x = 0. При этом предположении K'' (0) = 0 и (9) совпадает с (3), но K'' (0), очевидно, может и не быть нулем. Если же K ( x ) вблизи точки x = 0 — не аналитическая функция, то результат будет опять существенно зависеть от ее поведения в этой области, т. е. указанное нелепое следствие теории остается и в этом случае.

Указанный порок метода самосогласованного поля, как легко видеть, не связан с частными свойствами рассмотренного решения; еще до интегрирования видно, что поведение K ( x ) при x = 0 может играть существенную роль.