Эдуардо Лопец - Кеплер. Движение планет. Танцы со звездами.
- Название:Кеплер. Движение планет. Танцы со звездами.
- Автор:
- Жанр:
- Издательство:Де Агостини
- Год:2015
- ISBN:2409-0069
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдуардо Лопец - Кеплер. Движение планет. Танцы со звездами. краткое содержание
Иоганн Кеплер был глубоко религиозным человеком. Благодаря своему научному подходу он создал образ мира, отражающего всю полноту Божественной гармонии. Сформулированные им три закона движения планет дали изящное математическое объяснение наблюдениям Тихо Браге, подтвердили выводы Коперника и проложили путь открытиям Ньютона. Как и многие другие первопроходцы в науке, Кеплер занимался дисциплинами, которые сейчас мы называем эзотерическими, в частности, астрологией. Со временем он стал знаменитым астрологом: к его услугам прибегали принцы и короли. Но ни высочайшее покровительство, ни набожность ученого не спасли его от ужасных последствий религиозных войн, пылавших в то время в Европе.
Кеплер. Движение планет. Танцы со звездами. - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Максимальное расстояние от центра эллипса до его границы называется большой полуосью (обозначим ее как а). Минимальное расстояние от центра до его границы называется малой полуосью (b). Эксцентриситет орбиты, е, определяется с помощью формулы:
b=a(1-e2)½
Когда эксцентриситет е равен нулю, b = а, эллипс является окружностью, а его фокусы совпадают в центре окружности. Когда е приближается к 1, эллипс становится все более вытянутым, приближаясь к отрезку при е = 1.
Второй закон подразумевает, что чем ближе планета к перигелию, тем больше ее скорость по сравнению со скоростью в афелии. Перигелий – это самая близкая к Солнцу точка орбиты, афелий – самая дальняя. При круговой орбите нет ни афелия, ни перигелия, и в этом случае скорость движения планеты постоянна.
Рассмотрим третий закон Кеплера для круговой орбиты с нулевым эксцентриситетом. В этом случае сила гравитационного притяжения, действующая на планету, равна ее массе под действием центробежной силы (V²/d):
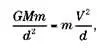
где G является константой всемирного притяжения, М – массой Солнца, d – расстоянием планеты до Солнца и V – ее скоростью. G и М постоянны независимо от рассматриваемой планеты:
V²d= константа. [1]
Принимая во внимание формулу, которая соотносит линейную скорость V с угловой скоростью Ω,
V = Ωd, [2]
и что период обращения Т связан с угловой скоростью:
Ω=2π/T
подставив [3] в [2] и затем [2] в [1], получаем:
d³/T² = константа. [4]
То есть куб средних расстояний между планетами пропорционален квадрату периода обращения.
Как видите, чтобы сделать такой вывод, нам хватило половины страницы. Почему же Кеплеру не хватило целой книги? Стоит учитывать, что для выведения третьего закона Кеплера мы использовали закон тяготения Ньютона, в то время еще неизвестный. Более того, на самом деле все было с точностью до наоборот: это Ньютон, изучив законы Кеплера, сформулировал закон всемирного тяготения таким образом, чтобы эти законы исполнялись. Приведенные рассуждения, справедливые только при круговой орбите, – лишь способ запомнить третий закон Кеплера.
Приведем таблицу расстояний планет до Солнца. В первой колонке указаны названия планет, во второй – расстояния от них до Солнца в миллионах километров, в третьей – те же расстояния, но с использованием астрономической единицы, которая равна расстоянию от Земли до Солнца. В четвертой эти величины округлены, чтобы их легче было запомнить, и, наконец, в пятом столбце указано время, необходимое лучу света для преодоления этих расстояний.
| Планета | В миллионах километров | В астрономических единицах | В астрономических единицах округленно | Время, необходимое лучу света для преодоления расстояния |
| Меркурий | 58 | 0,387 | 1/3 | 3 мин |
| Венера | 108 | 0,723 | 3/4 | 6 мин |
| Земля | 150 | 1 | 1 | 8 мин |
| Марс | 228 | 1,524 | 3/2 | 13 мин |
| Юпитер | 778 | 5,203 | 5 | 45 мин |
| Сатурн | 1427 | 9,539 | 10 | 1час 20 мин |
| Уран | 2870 | 19,18 | 20 | 2 часа 40 мин |
| Нептун | 4497 | 30,06 | 30 | 4 часа |
В примере [4] описан третий закон Кеплера: куб расстояний пропорционален квадрату периодов, коэффициент пропорциональности зависит от G и массы Солнца. Однако представим, что нам неизвестны эти константы и мы хотим использовать третий закон Кеплера для того, чтобы узнать периоды планет на основе приблизительных расстояний из таблицы. Все окажется очень простым, если измерять расстояние в астрономических единицах (а.е.). Мы можем преобразовать в этих единицах предыдущую формулу: Т = d 3/2то есть если мы хотим узнать период обращения (сидерический период) планеты, нам нужно возвести расстояние в куб и извлечь квадратный корень.
Рассмотрим в качестве примера Венеру. При расстоянии до Солнца, равном 3/4 а.е., ее период составит 0,65 земного года. Для Марса при расстоянии 3/2 а.е. после использования приведенной формулы получим 1,8 земного года. Для Юпитера при d = 5 а.е. получим, что один год на Юпитере равен приблизительно 11 земным. Естественно, точность расчетов можно повысить, использовав неокругленные значения.
Можно считать, что этот труд Кеплера – первая современная книга по астрономии. В ней приведены два из трех законов великого ученого, причем любопытно, что второй закон идет перед первым. Третий закон, как мы писали, появился только в Harmonices mundi, следующей книге. Astronomia nova была написана в 1605 году и опубликована в 1609-м. Ее полное название звучит так: Astronomia nova seu physica coelestis, tradita commentariis de motibus stellae Martis («Новая астрономия, или Физика небес, изложенная в комментариях о движениях звезды Марс»).
Хотя в названии говорится о планете Марс, законы Кеплера справедливы для всех планет. Марс оказался в названии потому, что Браге поручил Кеплеру вычислить орбиту именно Марса. Возможно, датчанин таким образом хотел просто проверить способности своего коллеги, ведь наблюдения за четвертой планетой Солнечной системы сложнее всего поддаются интерпретации. Можно считать большой удачей, что перед Кеплером была поставлена именно эта задача, потому что Марс с его большим эксцентриситетом наилучшим образом подходил для проверки догадок ученого.
Чтобы сформулировать первые два закона, Кеплеру пришлось прибегнуть к математически сложным методам, предвосхищающим дифференциальный анализ. Формируя оригинальные гипотезы, он часто использовал как религиозные соображения, так и результаты наблюдений, однако в этом случае победило уважение Кеплера к научным данным. Эта книга – образец строгого и объективного исследования, результат упорства и точности. Конечно, читать ее довольно сложно – как и многие другие работы ученого, – поскольку Кеплер тщательно развивает как свои ошибочные посылки, предшествующие решению, так и правильные итоговые умозаключения.

Иоганн Кеплер, портрет 1610 года, автор неизвестен.
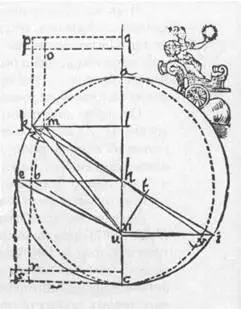
Страница из Astronomia nova (1609) на которой изображена работа Кеплера по расчету орбиты Марса. Этот рисунок иллюстрирует два его первых закона.

Страница из Harmonices mundi (1618) с музыкой, которую Кеплер считал свойственной звездам.
Итак, идеи Коперника и данные Тихо Браге наконец-то соединились. Казалось, теперь задача поддастся, однако это было не так. Погрешности при расчетах составили около 8' и хотя этот результат устроил бы любого другого астронома, Кеплер, используя данные Тихо Браге с погрешностью менее 2' требовал от себя такой же точности.
Читать дальшеИнтервал:
Закладка:









