Хоакин Наварро - Том 37. Женщины-математики. От Гипатии до Эмми Нётер

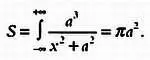
Эта площадь в четыре раза больше площади окружности, на основе которой определяется кривая. Отсюда следует вывод, который может показаться парадоксальным: кривая бесконечной длины ограничивает фигуру конечной площади. Если мы будем вращать кривую вокруг оси абсцисс, то объем полученного тела вращения будет равен

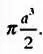
Центр тяжести кривой расположен на оси у (это ось симметрии кривой) в точке ( О, а /4).

Верзьера Аньези известна прежде всего благодаря своему названию, но сегодня она редко используется в высшей математике (вместе с коноидом Плюкера и зонтиком Картана). Возможно, наиболее примечательной областью ее применения является анализ излучения света и статистических феноменов, связанных с так называемым распределением Коши — распределением вероятностей, функция плотности для которого в простейшем случае выглядит так:

* * *

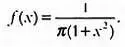
ВСЕ ЕДИНО, ДИФФЕРЕНЦИРОВАНИЕ — ТО ЖЕ, ЧТО ИНТЕГРИРОВАНИЕ

Если мы посмотрим на внушительное здание математического анализа под определенным углом, то сразу же станет понятно: если нам известны все мельчайшие мгновенные изменения переменной, то при помощи некоторой суммы мы сможем вычислить ее общее изменение. Этот интуитивно понятный вывод естественным образом приводит к определению дифференцирования и интегрирования.

Тысячи страниц «Основ анализа для итальянской молодежи» посвящены общей теме — дифференциальному и интегральному исчислению. Кроме того, в этой книге делается упор на том, что дифференцирование и интегрирование — обратные операции. Сегодня это утверждение кажется очевидным и рассматривается в школьном курсе анализа одним из первых, но в 1748 году все было не так просто.

Если использовать современные термины — более точные, но, к сожалению, более пространные, — то утверждение «интегрирование и дифференцирование — взаимно обратные операции» будет звучать так: если f— функция, непрерывная на отрезке [ а , Ь ], и задано следующее соотношение

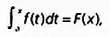
то функция Fявляется дифференцируемой на отрезке [ а , Ь ] (она называется первообразной функции f) и F( х ) = f( x ). Кроме того, если функция Fдифференцируема на отрезке [ а , Ь ] и F'( х ) = f( x ), то

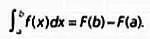
Это двойное утверждение получило название основной теоремы анализа. Ее практически полностью сформулировал Исаак Барроу(1630–1677) , щедро уступивший Ньютону должность лукасовского профессора Кембриджа.

* * *

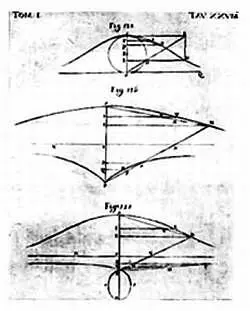
Верзьера Аньези на заключительных страницах первого тома «Основ анализа».

Предлагаем вам провести небольшой эксперимент с карманным калькулятором — лучше слегка устаревшим. Этот эксперимент не нов, и если он уже знаком вам, пропустите следующий абзац. Может быть, вы его видели в одной из серий «Симпсонов». Как вы, наверное, знаете, все происшествия, которые случаются с Гомером Симпсоном, обычно оканчиваются неудачей, поэтому не говорите, что мы вас не предупреждали!

В руки Гомеру попало следующее предполагаемое равенство

1782 12+ 1841 12= 1922 12.

Гомер, который по определению не знает математики, решает проверить это равенство: он берет старый калькулятор, который позволяет выполнять только элементарные действия и показывает 10 цифр результата, и находит сумму

1782 12+ 1841 12.

Затем он вычисляет 1922 12и — сюрприз! — на экране высвечиваются те же 10 цифр. Прощай, знаменитая теорема Ферма — мы нашли контрпример:

1782 12+ 1841 12= 1922 12.

Или нет? Истина восторжествует, если мы возьмем современный калькулятор — станет очевидно, что разность этих чисел не равна нулю. Если этот калькулятор способен работать с достаточным числом десятичных знаков, то мы получим, что разность этих чисел равна 700212234530608691501223040959 — это очень малое, ничтожное число, практически равное нулю по сравнению с исходными числами (они имеют по 40 знаков), но его достаточно для того, чтобы гипотеза Ферма — сегодня она носит статус теоремы — устояла. Однако в XIX веке теорема Ферма еще не была доказана, и математики лишь предполагали ее истинность. Согласен с ними был и господин Антуан Огюст Леблан, точнее говоря, Софи Жермен — женщина, взявшая себе этот псевдоним. Господин Леблан в действительности существовал и был настоящим мужчиной с усами. Софи Жермен всего лишь подписывала письма его именем. Похоже, настало время разъяснить все вышесказанное. Итак, кто такая Софи Жермен?

Неженская целеустремленность

Софи Жермен родилась в Париже и была средней из трех сестер в семье, которую можно назвать богатой, но не знатной. Ее отцом, как считает большинство историков, был преуспевающий торговец шелками, который в итоге возглавил Банк Франции. Софи спокойно пережила сложные времена Великой французской революции, в ходе которой по той или иной причине или вовсе без причин множество людей лишилось своих постов и даже жизни. Софи провела годы Террора, сражаясь не с Робеспьером, а с устройством мира, в котором, казалось, не было места женщине, желавшей заниматься математикой. Как мы уже не раз отмечали, в знатных семьях считалось хорошим тоном, если женщина немного разбиралась в науке, чтобы просто поддержать беседу. Но для женщины из буржуазной семьи стремление разбираться в науке считалось глупостью: она не должна была покидать священный мир ниток, иголок, пианино, акварелей и детей. Доказательством этому послужит книга той эпохи под названием «Ньютонизм для дам». В одной из глав аристократическая пара обсуждает закон всемирного тяготения Ньютона. В диалоге, который можно назвать сюрреалистичным, маркиза проводит аналогию, которая привела бы самого Ньютона в ужас: «Этот закон тяготения верен и для любви — после восьми дней разлуки любовь становится в шестьдесят четыре раза сильнее». Но довольно об этой книге.

Софи начала интересоваться математикой, когда прочла в книге Монтукля, взятой из отцовской библиотеки, о гибели Архимеда от рук римского солдата: «Оставь меня в покое и не трогай моих чертежей», — сказал Архимед солдату, который предложил мудрецу пройти с ним. Возмущенный непочтительностью Архимеда, солдат зарубил его мечом. Софи задумалась: если ученый пожертвовал жизнью ради чертежей, в них, наверное, было сокрыто нечто очень ценное. В чем же заключается ценность геометрии, сравнимая с ценностью самой жизни?