Хоакин Наварро - Том 37. Женщины-математики. От Гипатии до Эмми Нётер

Третья причина, по которой труд Аньези стоит особняком, носит более глубокий характер. Европа в те годы была разделена на два лагеря: островной, то есть радикальных сторонников теорий и обозначений британского ученого Исаака Ньютона, и континентальный — лагерь сторонников Лейбница. Каждый принадлежал к тому или иному лагерю, подобно тирийцам и троянцам, магометанам и христианам или современным футбольным фанатам. Марии удалось решить очень сложную на тот момент задачу: объединить в своей книге обе точки зрения (по сути, эквивалентные), взяв лучшее из каждой. С другой стороны, Мария сделала упор на том, что две основные операции в математическом анализе — дифференцирование и интегрирование — являются взаимно обратными, и это очень современный подход.

Книга Аньези считалась наиболее понятной и полной со времен публикации труда маркиза Лопиталя, изданного более чем 50 годами ранее. Важно и то, что труд Марии иллюстрирован гравюрами, которые делают изложение куда более доходчивым. В те времена, когда искусство книгопечатания еще только развивалось, использование гравюр в учебнике было настоящей роскошью. Публикацию оплатила семья Аньези. Мария перевезла печатные машины к себе домой, чтобы полностью контролировать процесс. Книга имела широкие поля, была отпечатана большим и легко читаемым шрифтом.

«Основы анализа для итальянской молодежи» сразу после публикации не приобрели особую известность — математический анализ в те годы не был популярен, а кроме того, научным работам, в которых не излагались новые открытия, в те годы не придавалось большого значения. Следует понимать, что Мария не ставила целью написать целый трактат, а хотела создать учебник по анализу, тщательно отобрав множество примеров. Но со временем ее книга стала известной и была переведена на английский и французский языки. Французский перевод был выпущен достаточно поздно, так как редакторы дополнили оригинал рядом тригонометрических понятий, которых, по их мнению, не хватало в тексте, и оказались правы.

История английского перевода заслуживает особого рассказа. Его автором стал кембриджский преподаватель Джон Колсон, искренний ценитель труда Марии, к сожалению, плохо знавший итальянский язык. В конце первого тома была изображена и подробно рассмотрена особая кривая, которую первым описал геометр Гвидо Гранди(1671–1742) . Гранди назвал свою кривую curva versoria , применив морской термин, обозначавший веревку, которая позволяла поворачивать парус.

Слово versoria происходит от латинского vertere , и Гранди провел аналогию между этим латинским словом и выражением sinus versus (синус-верзус, или обращенный синус). Все это стало причиной ошибки в переводе. Сегодня считается, что Колсон при переводе перепутал словосочетание la versiera di Agnesi со словами la awersiera di Agnesi . Эта ошибка также была бы не слишком заметной, если бы слово awersiera не означало «ведьма» или «колдунья». В результате во всех англоязычных книгах по математике эта кривая называется «ведьма Аньези» ( The witch of Agnesi ). Это дьявольское название произвело фурор, и Мария Аньези (которая, как мы уже говорили, постриглась в монахини) стала известна в мире математики не только как автор «Основ анализа», но и по этому яркому и не вполне богоугодному названию кривой. Ошибка распространялась все шире, и ход событий было уже не остановить. Одна женщина-композитор даже написала музыкальную пьесу для семи инструментов под названием The witch of Agnesi .

Несмотря на эти досадные неточности, труд Колсона, который умер много лет спустя, так и не дожив до публикации этого перевода, был крайне важен. Он взялся за работу, движимый искренним восхищением красотой книги Аньези, и даже потрудился (и совершенно напрасно) заменить обозначения Лейбница сумбурной нотацией Ньютона. Впрочем, чего еще можно было ожидать от островного математика?

История оказалась жестокой и несправедливой. Труд Аньези занимает более 20 томов в Амброзианской библиотеке Милана, но если сегодня мы спросим какого-нибудь ученого, знакома ли ему фамилия Аньези, он если и ответит положительно, то наверняка упомянет «ведьму Аньези», а не женщину-математика и ее удивительный вклад в науку.

Верзьера Аньези

Верзьеру Аньези рассматривали еще Пьер Ферма(1601–1665) в 1630 году и Гвидо Гранди — в 1703-м. Эта кривая определяется как геометрическое место точек, обладающих общим свойством, которое формулируется не самым простым образом.

Рассмотрим декартову систему координат и построим в ней окружность диаметра а с центром в точке С , расположенной на вертикальной оси. Обозначим через О и Т соответственно нижнюю и верхнюю точки окружности, лежащие на оси у .

Верньера Аньези определяется следующим образом: выберем точку окружности А и проведем прямую ОА , которая пересечет в точке В прямую, образованную точками с ординатой а (эта прямая параллельна горизонтальной оси координат и проходит через точку Т ).

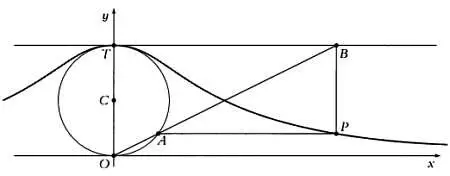
Соответствующей точкой верзьеры Аньези будет точка Р , отмеченная на иллюстрации: ее ордината равна ординате точки А , абсцисса — абсциссе точки В . Объяснить построение верзьеры Аньези сложнее, чем понять его основной принцип. Полученная кривая по своей форме в самом деле напоминает веревку, с помощью которой поворачивается парус.

Уравнение этой кривой в декартовых координатах выводится совершенно иначе, но также без особых сложностей: проведя некоторые расчеты, любой способный старшеклассник покажет, что искомое уравнение выглядит следующим образом:

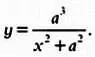
Верзьера Аньези — кубическая кривая. Если диаметр исходной окружности равен единице, то уравнение верзьеры Аньези будет особенно простым:

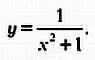
Определить параметрическое представление этой кривой сложнее, и с этой задачей справится уже не каждый. Но тот же самый способный старшеклассник, приложив определенные усилия, получит выражения

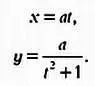
Это параметрическое представление кривой с параметром t . В завершение нашего рассмотрения верзьеры Аньези укажем, что симметричные точки с абсциссами

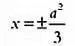
являются точками перегиба, в которых кривая «дьявольски» меняет направление и «смотрит» уже не вниз, а вверх. Вычислив площадь S фигуры, ограниченной этой кривой и горизонтальной осью, с помощью интегрального исчисления, получим