Хоакин Наварро - Том 37. Женщины-математики. От Гипатии до Эмми Нётер

Основных алгебраических структур, которые рассматриваются как множества с одной или несколькими операциями, много. Мы ограничимся тем, что рассмотрим структуры, на которых определены две операции, oи •. Этими операциями часто оказываются +и •. Порой требуется так называемый третий закон внешней композиции ( а иногда и больше), но мы рассмотрим только простейшие случаи. Вместо того чтобы постоянно использовать слова «является элементом», заменим их символом .

Группой называется множество элементов А с определенной на нем операцией o, которая удовлетворяет трем следующим условиям:

1) существует нейтральный элемент n такой, что n о а = а о n = а для любого a А;

2) для каждого а А существует обратный элемент а -1такой, что а о а -1= а -1о а = n ;

3) для любых a, b, с А выполняется свойство ассоциативности, согласно которому ( а о Ь ) о с = а о ( Ь о с ).

Группа называется коммутативной, или абелевой (в честь норвежского математика Нильса Хенрика Абеля), если для любых a, b А определенная нами операция обладает коммутативностью, то есть выполняется соотношение а о Ь = b о а .

Если на группе определена операция сложения (+), то элемент, обратный а , обозначается — а и называется противоположным. Нейтральный элемент в этом случае обозначается 0.

Если на группе определена операция умножения (), то элемент, обратный а , обозначается 1/ а . Нейтральный элемент в этом случае обозначается 1.

4) для любых а, Ь, с А справедливо ( а Ь ) с = а ( Ь с ).

Операции о и связаны друг с другом свойством дистрибутивности относительно:

5) а ( Ь о с ) = ( а b ) о ( а с ).

Кольцо — это коммутативная группа, на которой определена еще одна операция обладающая свойством ассоциативности:

Примерами колец являются натуральные числа 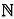, целые числа , рациональные числа 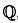, вещественные числа 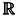и комплексные числа 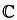(вне зависимости от определенной для них модальной арифметики). Многочлены также образуют кольца.

В мире колец операция ообладает коммутативностью аналогично операции сложения, поэтому она обозначается знаком +. Операция (для простоты будем предполагать, что она также обладает коммутативностью) обозначается знаком ·, подобно умножению.

Подгруппой или подкольцом А будет любое подмножество, которое будет оставаться группой или кольцом, если ограничить операции оили этим подмножеством. Идеал — особое подкольцо: это подкольцо В 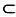А такое, что любое произведение b В и любого другого элемента, принадлежащего В или нет, будет принадлежать В . Идеалы можно складывать и перемножать. Результатами сложения и умножения идеалов также будут идеалы. Понятие идеала возникло как обобщение понятия числа. Для двух данных идеалов I и J имеем:

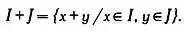
Определить идеал IJ несколько сложнее. Это идеал, порожденный всеми произведениями ху , где х I, у J . Пересечение всех идеалов, содержащих подобные произведения, называется порожденным идеалом.

Областью целостности называется кольцо А , на котором для операции · не существует так называемых делителей нуля. Иными словами, на этом кольце не существует элементов а и b таких, что аb = bа = 0.

В этом случае кольцо А является коммутативным и содержит единичный элемент, то есть для операции определен нейтральный элемент, играющий роль единицы:

а 1 = а .

Теперь рассмотрим область целостности А без 0. Обозначим ее через А * = А |(0). Если операция ·определяет на А * коммутативную группу, то А называется полем. Если А * не является коммутативной, то А называется телом. Не стоит пугаться подобных сложностей: если кольцо А конечно, то оно коммутативно согласно знаменитой теореме Веддербёрна. Если кольцо А бесконечно, то наступает раздолье для алгебраистов.

Рассмотрим А-модули — редчайший вид современного алгебраического мира. Чтобы определить левый А-модуль, нам потребуются кольцо с единицей А и коммутативная группа М . Действия с элементами a, b А и элементами М ( m, n М ) определяются следующим, вполне обычным образом:

1. ( ab ) m = а ( Ьm )

2. ( а + b ) n = am + bm

3. а ( m + n ) = am + аn

4. 1 m = m .

Аналогично определяется правый А-модуль; коммутативный модуль (или просто A-модуль) — это модуль, который является правым и левым одновременно. Если А — поле, то A-модуль называется векторным пространством. Если для векторов векторного пространства определена операция умножения, имеем «алгебру». На этом мы остановимся. Хотя приведенные нами определения элементарны, вполне возможно, что читатель не назовет элементарным этот раздел.

Большая часть научной работы Эмми Нётер была посвящена кольцам и идеалам — алгебраическим структурам, над которыми она работала многие годы. Почему же Нётер уделяла им такое внимание?

Многие объекты, с которыми работают математики, представляют собой кольца: так, кольцами являются множество целых чисел и его последовательные расширения — , и . Кольцами также являются многочлены одной переменной с коэффициентами из вышеуказанных колец [X], [X], [X] и [X]. Аналогично кольцами являются многочлены нескольких переменных [X 1, Х 2…., X n], [X 1, Х 2…., X n], [X 1, Х 2…., X n], и [X 1, Х 2…., X n]. А также сходящиеся ряды — короче говоря, много чего еще.

Но что такое идеалы и почему они получили столь романтичное название? Совершим небольшой экскурс в историю математики. Рассмотрим в качестве примера квадратичное целое [√-5] или [i√5], что аналогично. Это множество чисел вида а + Ь √-5, где а и Ь — целые числа. Иными словами,

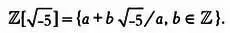
[√-5] — кольцо (убедитесь в этом), но здесь, говоря математическим языком, мы вступаем в запретную зону. Мы привыкли к стандартным свойствам делимости и к тому, что разложение числа на простые множители всегда является единственным. К примеру, рассмотрим число 21. Имеем 21 = 3·7 и на этом разложение на множители заканчивается: 21 можно разложить на простые множители единственным способом, и этими множителями будут 3 и 7. Это утверждение следует из основной теоремы арифметики: на множестве разложение любого числа на простые множители является единственным. На множестве [√-5] это утверждение уже не будет выполняться: здесь мы можем разложить 21 на простые множители двумя способами: