Хоакин Наварро - Том 37. Женщины-математики. От Гипатии до Эмми Нётер

Диофантовыми называются полиномиальные уравнения вида

Р( х 1, х 2 , …, х n ) = 0

с решениями и коэффициентами на множестве . Проблема Гильберта под номером 10 звучала так: существует ли алгоритм или метод, позволяющий определить, имеет ли решения произвольное диофантово уравнение? В конце концов в 1970 году было доказано, что такого алгоритма не существует. Десятая проблема Гильберта допускает бесконечное множество случаев. Известны подмножества случаев, для которых искомый спасительный алгоритм существует, однако в задаче требуется найти универсальный алгоритм для всех возможных случаев. К примеру, алгоритм Евклида позволяет решить диофантовы уравнения вида

ax ± by = с ,

но не уравнения произвольного вида (указанные уравнения имеют решения тогда и только тогда, когда НОД ( а, Ь ) является делителем с ). Путь к решению десятой проблемы Гильберта непрост, и многие не сразу поймут его. Но мы все же попытаемся описать ее решение, пусть и очень поверхностно.

В 1950 году Джулия Робинсон, применив некоторые свойства уравнения Пелля, не смогла доказать, что определенное числовое множество, которое мы обозначим JR в честь Джулии Робинсон (его нельзя построить, но можно определить в терминах общей арифметики), является диофантовым (см. врезку, посвященную Алану Тьюрингу), но не вычислимым. Множество JR обладало некоторыми интересными свойствами — в частности, его элементы возрастали по экспоненциальному закону.

Доказать указанное свойство не удалось, однако эта гипотеза с высокой вероятностью считалась истинной. Далее будем называть эту гипотезу гипотезой JR . В 1959 году Мартин Дэвис и Хилари Патнем доказали, что при определенных условиях из гипотезы JR следует очень важный результат: любое рекурсивно перечислимое множество является диофантовым. Если выполняются начальные условия и гипотеза JR , то десятую проблему Гильберта можно считать решенной, и ответ на нее будет отрицательным.

* * *

НЕМНОГО ТЬЮРИНГА

При решении проблем разрешимости и вычислимости, а также логических задач обычно используются машины Тьюринга. Эти машины, придуманные английским ученым Аланом Тьюрингом (1912–1954), в действительности представляют собой идеальные математические абстракции вычислительных машин с бесконечной памятью. Представьте себе ящик с входным и выходным отверстиями, через которые проходит бумажная лента, разделенная на прямоугольные ячейки. В каждой ячейке записана цифра — 0 или 1. В крышке ящика есть смотровое отверстие, через которое в любой момент можно увидеть, какая цифра записана в ячейку. На каждом шаге цифру в ячейке можно заменить на 0 или 1. Аналогично, можно определить, куда следует переместить считывающее устройство на следующем шаге: влево или вправо. Новая записанная цифра и новое состояние машины зависят от текущего состояния машины, а следующий шаг (и следующее состояние) указаны в программе, записанной в управляющем устройстве. Программы различных машин Тьюринга отличаются. Прекратит ли машина работу, зависит оттого, что указано в программе. Может показаться, что от столь простого устройства не стоит ждать многого, однако потенциал машины Тьюринга огромен.

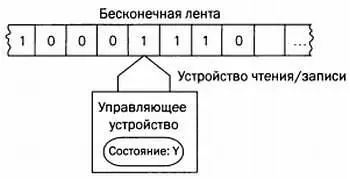
Простейшая схема работы машины Тьюринга.

Далее приведены три определения, тесно связанные с работами Джулии Робинсон и диофантовыми уравнениями. Они приводятся отдельно, так как используются в рассуждениях, самих по себе достаточно сложных.

— Перечислимое множество (по историческим причинам также называется рекурсивно перечислимым): множество целых чисел Lназывается перечислимым, если существует машина Тьюринга такая, что если ввести в нее целое число, она остановится на 1, если указанное число принадлежит LЕсли указанное целое число не принадлежит L, машина может остановиться на 0 или не остановиться никогда.

— Вычислимое множество: множество Сназывается вычислимым, если существует программа машины Тьюринга такая, что для любого введенного целого числа машина останавливается на 1, если это число принадлежит С, в противном случае — на 0. Чуть менее понятное, но эквивалентное определение вычислимого множества таково: множество Сназывается вычислимым тогда и только тогда, когда Си его дополнение С ― являются перечислимыми. Очевидно, что любое вычислимое множество является перечислимым, но не наоборот.

— Диофантово множество: множество целых чисел Dназывается диофантовым, если его можно определить с помощью многочлена Р ( x 1 , x 2 , x t ) от переменных d, t, x 1, x 2…., x t>= 1 с целыми коэффициентами такого, что Робращается в ноль при присвоении целых значений x 1, x 2…., x tтогда и только тогда, когда dравно одному из элементов множества D.

Алан Тьюринг.

* * *

Всего годом позже в игру вступила Джулия Робинсон: ей удалось упростить задачу и устранить неудобные начальные условия, описанные Дэвис и Патнем. Ситуация была такова: если возможно множество вида JR, то десятая проблема Гильберта будет решена. Достаточно найти диофантово уравнение с определенными решениями, возрастающими экспоненциально, но это уравнение ускользало от математиков. Открытие было совершено в 1970 году, спустя почти 30 лет поисков. Юный математик Юрий Матиясевич из Советского Союза представил колоссальную систему диофантовых уравнений:

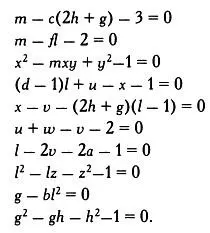
Если мы возведем обе части всех этих уравнений в квадрат и сложим их почленно, то получим одно уравнение, которое будет иметь те же решения на множестве натуральных чисел, что и вся система. Полученное уравнение будет удовлетворять необходимым начальным условиям.

Матиясевич получил приведенные выше десять уравнений не случайно: он использовал в работе весьма остроумные методы. Ключевую идею математик заимствовал из теоремы, доказанной в 1942 году и затерянной на страницах третьего издания старенькой книжечки под названием «Числа Фибоначчи» советского математика Николая Воробьева. Для десяти приведенных выше уравнений выполняется равенство v = F 2 м , где F i— i -e число Фибоначчи. Интересно, что эта теорема приводится только в третьем издании книги Воробьева и отсутствует в первых двух.