Ниал Фергюсон - Площадь и башня [Cети и власть от масонов до Facebook]

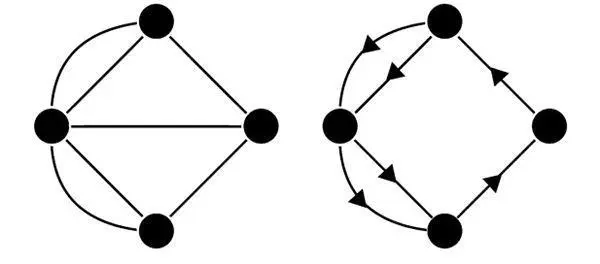
Илл. 5. Упрощенная схема Эйлеровой задачи о кёнигсбергских мостах. Задачу можно решить, только убрав грань в середине (то есть мост, соединяющий два острова, на илл. 4).

В середине ХХ века произошел и существенный прогресс в нашем понимании совокупных свойств сети, которые зачастую остаются незаметными с точки зрения любого отдельного узла. Р. Дункан Люче и Альберт Перри из Массачусетского технологического института предложили использовать коэффициенты “кластеризации” для измерения той степени, в которой связаны между собой узлы в группе, причем крайним случаем считается клика, внутри которой каждый узел связан со всеми остальными в группе. (Строго говоря, коэффициент кластеризации показывает количественное соотношение полносвязанных общественных триад, то есть таких, в которых каждый член любой троицы связан с двумя остальными.) Плотность сети – похожий критерий взаимосвязанности.

Важность таких единиц измерения стала очевидной в 1967 году, когда социальный психолог Стэнли Милгрэм провел свой знаменитый эксперимент. Он направил письма произвольно выбранным адресатам, жившим в Уичито, штат Канзас, и в Омахе, штат Небраска. Получателей просили переслать письмо напрямую намеченному конечному адресату – соответственно, жене одного студента-богослова из Гарварда и одному биржевому маклеру в Бостоне, – если они лично знают этих людей, или же переслать письмо кому-нибудь, кто, по их мнению, может знать конечного адресата, при условии, что они сами коротко знакомы с посредником. А еще их просили отправить Милгрэму открытку отслеживания и в ней рассказать о том, что именно они сделали. В целом, по сообщению Милгрэма, 44 из 160 писем из Небраски в итоге были доставлены по назначению [137] Milgram, ‘Small World Problem’. . (Более позднее исследование наводит на предположение, что таких писем было всего 21 [138] Watts, Six Degrees, 134. См. также Schnettler, ‘Structured Overview’. .) Законченные цепочки позволили Милгрэму подсчитать количество посредников, задействованных для того, чтобы доставить письмо по назначению: в среднем оно равнялось пяти [139] Barabási, Linked , 29. . Это открытие предвосхитил венгерский писатель Фридьеш Каринти в рассказе “Звенья цепи” (Láncszemek) , напечатанном в 1929 году: там главный герой держит с приятелями пари, что сумеет связаться с любым человеком на Земле, кого бы они ни назвали, всего через пятерых общих знакомых, из которых ему самому нужно лично знать всего одного. К этой же задаче подступались и другие исследователи, проводившие эксперименты независимо друг от друга, – в частности, политолог Итиэль де Сола Пул и математик Манфред Кохен.

Сеть, в которой два узла связаны через пятерых посредников, имеет шесть ребер (звеньев). Выражение “шесть рукопожатий” [буквально – шесть степеней разделения] прижилось лишь после появления в 1990 году одноименной пьесы Джона Гуэра, но у него имелась долгая предыстория. Как и представление о том, что “мир тесен” (так назвали диснейлендовский аттракцион, придуманный в 1964 году), или техническое понятие близости, эта фраза очень емко подытоживает ощущение взаимосвязанности, усилившееся в середине ХХ века. Эта тема разыгрывалась во множестве вариаций: шесть шагов до Марлона Брандо, шесть шагов до Моники Левински, шесть шагов до Кевина Бейкона (этот вариант даже превратился в настольную игру [140] Имеется в виду игра “Шесть шагов до Кевина Бейкона”, в которой надо не более чем за шесть шагов установить связь между актером Кевином Бейконом и неким загаданным актером. (Прим. ред.) ), шесть шагов до Луизы Вайсберг (матери одного из друзей Малкольма Гладуэлла [141] Гладуэлл Малькольм (род. 1955) – известный канадский журналист, автор нескольких книг-бестселлеров. (Прим. ред.) ), а еще – если обратиться к научным аналогам этих игр – шесть шагов до математика Пала Эрдёша, который, как известно, заложил основы теории сетей [142] Jennifer Schuessler, ‘How Six Degrees Became a Forever Meme’, The New York Times , 19 April 2017. . Недавно проведенные исследования позволяют предположить, что количество этих рукопожатий сейчас скорее ближе к пяти, чем к шести, а это, в свою очередь, наводит на мысль о том, что с 1970-х годов технический прогресс, пожалуй, принес не такие уж разительные перемены в нашу жизнь, как принято считать [143] Jackson, Rogers and Zenou, ‘Connections in the Modern World’. . Впрочем, для директоров тысячи самых крупных компаний, по версии журнала Fortune, это число составляет 4,6 [144] Davis, Yoo and Baker, ‘The Small World of the American Corporate Elite’. . А для пользователей сети Facebook оно составляло 3,74 в 2012 году [145] Lars Backstrom, Paolo Boldi, Marco Rosa, Johan Ugander, and Sebastiano Vigna, ‘Four Degrees of Separation’, 22 June 2012. и только 3,57 – в 2016-м [146] Smriti Bhagat, Moira Burke, Carlos Diuk, Ismail Onur Filiz, and Sergey Edunov, ‘Three and a Half Degrees of Separation’, 4 February 2016. .

Это открытие оказывается очень занимательным, потому что обычно мы думаем, что наши дружеские связи охватывают относительно небольшие группы людей или кружки похожих людей, единомышленников, которые существуют обособленно от других групп, куда входят совсем другие люди – непохожие на нас, но сходные между собой. А если всех нас в действительности отделяет от Моники Левински лишь шесть рукопожатий, то это объясняется явлением, которому стэнфордский социолог Марк Грановеттер дал парадоксальное название – сила слабых связей [147] Granovetter, ‘Strength of Weak Ties’. . Если бы все связи были похожи на крепкие гомофилические узы, какие связывают нас с нашими близкими друзьями, то мир неизбежно оказался бы фрагментирован. Но более слабые связи – со знакомыми, с которыми у нас уже меньше сходства, – играют ключевую роль в феномене, который описывается фразой “мир тесен”. Изначально Грановеттера интересовал вопрос о том, почему людям, которые ищут работу, чаще помогают знакомые, чем близкие друзья, но затем ему в голову пришла мысль, что в обществе с относительно малым количеством слабых связей “новые идеи будут распространяться медленнее, научные дерзания будут натыкаться на помехи, а подгруппам, разделенным по принципу расовой, национальной или территориальной принадлежности или по иным критериям, будет сложно достичь взаимопонимания” [148] Granovetter, ‘Strength of Weak Ties Revisited’, 202. . Иными словами, слабые связи – это жизненно важные мосты, переброшенные между различными кластерами или группами, которые иначе не были бы никак связаны друг с другом [149] См. также Tutic and Wiese, ‘Reconstructing Granovetter’s Network Theory’. Недавние исследования с использованием данных Facebook в целом подтверждают тезис Грановеттера: Laura K. Gee, Jason Jones and Moira Burke, ‘Social Networks and Labor Markets: How Strong Ties Relate to Job Finding on Facebook’s Social Network’, 13 January 2016. .