Мартин Буркхардт - Краткая история цифровизации [litres]

Его обращение к математике после глубокого интереса к классическим и современным языкам связано с откровением, которое он испытал в 17 лет. В этом откровении не было ничего сверхъестественного – не сравнить с опытами Чарльза Бэббиджа, который пытался выманить дьявола из своего царства, очертив себя кругом из крови (тот опыт провалился, а сам Бэббидж стал веселым агностиком). В случае Буля не было ни искушения, ни драмы, просто в очередной раз проходя по тропинке через луг, он вдруг задался вопросом: почему люди обозначают такие разные вещи, например яблоки и груши, одними и теми же знаками – в этом случае цифрой 3? Получается, в человеческом мозге есть какая-то природная сила, которая сопровождает любое осознание и любую мысль, позволяя одинаковым образом считать и яблоки, и груши?

В самой постановке вопроса нет ничего революционно нового: многие поколения математиков до Буля были убеждены в том, что числа – это что-то априорное, изначально присущее нашему рассудку ровно в той же мере, что и чувство прекрасного, доброго и хорошего. Однако в этой точке зрения есть одна загвоздка: мысль о том, что каждый человек – математик от рождения, может, пожалуй, возмутить какого-нибудь математика, притом что вся остальная общественность вряд ли сильно впечатлится этим. И потом – такое утверждение порождает серьезные логические проблемы. Скажем, человек от рождения знает о числе 3. А о числах 4001 и 41627?

А об отрицательных числах? А об иррациональном и трансцендентном числе π?

Фокус Буля состоял в том, что он вообще не пускался в эти софистические рассуждения, а посмотрел на мир по-новому взглядом, свободным от всяческих предрассудков. Он спросил себя, может ли быть такое, что эта природная сила еще никем не была найдена и представляла собой нечто неосознанное. При этом «неосознанное» в его интерпретации было чем-то крайне простым, – тем, что делает маленький ребенок, когда прячет, а потом достает игрушку: «Где зайчик? Вот он!»

Буль понял, что законы мышления опирались на факт присутствия или отсутствия предмета, и это прозрение имело далеко идущие последствия, ведь, начав считать в яблоках и грушах, он недолго думая отправил прежний мир чисел на свалку истории. Буль размышлял следующим образом: если все, что существует в мире, бросить в один котел, то это можно будет обозначить одним словом – единством, вселенной или универсумом. Что же останется после того, как мы уместим все в один котел? Правильно – останется ничто. Так он сформулировал два полюса той парадигмы, которую мы не осознаем, но всегда учитываем: «присутствие» и «отсутствие», «всё» и «ничто».

И в этот момент Буль снова вводит в рассмотрение числа, но уже не для вычислений. Напротив, он придает им новое, почти философское значение: единица теперь означает «универсум», а ноль – «ничто». Тут, конечно, возникает вопрос: чего же он добился этим? Давайте возьмем в качестве примера бумажник, который я вчера положил на стол, а сегодня его там нет. Поможет ли мне булева система найти его? Раз я уже всюду обыскался своего бумажника, это значит, что я могу в точности представить его себе. Рассуждая от обратного, можно помыслить и противоположное, то есть универсум без моего бумажника.

Таким образом, мы только что описали искомый бумажник, который для простоты будем называть X, и можем преобразовать это описание в уравнение:

1 – не-X (то есть вселенная без того, что не является моим бумажником) = 0 + X (то есть ничто плюс бумажник).

Этим приемом Булю удалось добиться того, что было невозможно в классической математике, потому что теперь вычисления стало можно производить с чем угодно. В определенном смысле такой способ мышления значительно точнее, чем традиционный подход, основанный на числах: ведь когда я ищу потерянный бумажник, я не думаю о красно-коричневом кожаном бумажнике шириной 12,5 см, высотой 9 см, глубиной 2 см, содержащем ровно 67 евро и 58 центов. Нет, я просто ищу и не нахожу знакомый мне предмет. В этот момент идентификация предмета происходит не через числа, а через восприятие – то есть через осознание того факта, что нужная мне вещь отсутствует на привычном месте. Всё это скорее роднит булеву логику с обычной операцией поиска, а не с операцией подсчета.

Если вы успели уследить за моими объяснениями, то уже начинаете понимать, что идеи Буля были такими же революционными, каким было открытие электрического флюида. Они позволяли описывать любой объект и любое соотношение объектов в логике нулей и единиц: бумажник (есть или нет), состояние двери в квартиру (открыта или закрыта), количество сорванных с дерева яблок или груш в корзине. Числа передают только один из аспектов окружающего мира (квант), а булева логика позволяет описывать все мыслимые качества: голос, который приглашает покупателей в магазин, данные о местоположении кита или движение руки (которое за человеком тут же повторяет робот). Это даже не математика, это шаг к созданию совершенно новой универсальной письменности. Какова же наименьшая единица этой письменности? В логике наличия и отсутствия это уже не цифра, а минимально возможная единица значения – бит.

Как известно, бит может быть «включен» или «выключен», что определяет его булево значение: наличие или отсутствие. Как же преобразовать такой бит в число? Просто взять и выразить его числом. При этом численное значение – далеко не единственное возможное. Если мне захочется, бит я могу представить и в виде закрашенного квадратика (■) или в виде буквы, с которой начинается следующий абзац. Ясно одно: в булевой алгебре ничто больше не является тем, что собой представляет. Любая сущность в этой логике – всего лишь последовательность битов. Теперь давайте разберемся, как преобразовать предмет в биты. Начнем с чисел, которые Буль выносит за рамки своего рассуждения о наличии и отсутствии, о «всем» и «ничем». Что произойдет, если представить бит в виде числа? Во-первых, я не смогу даже досчитать этими числами до двух, ведь «невключенный» бит интерпретируется как «ничто», то есть 0, а «включенный» как 1.

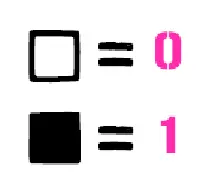
Чтобы досчитать до трех, нам потребуется два бита:

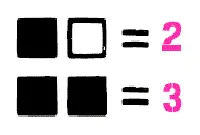
Если добавить еще один бит, то мы уже продвинемся до семи.

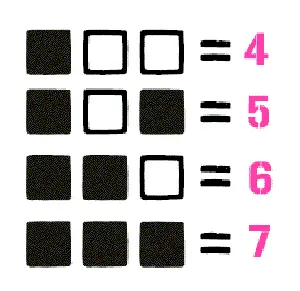
Доступное нам пространство для вычислений удваивается с каждым битом, как в задаче о шахматной доске, где за первую клетку изобретатель шахмат запросил у короля одно рисовое зернышко, а за каждую следующую вдвое больше, чем за предыдущую. Если тремя битами можно записать восемь чисел (от 0 до 7), то четырьмя битами – уже 16 чисел, пятью битами – 32 числа, а 64 бита уже позволяют нам оперировать невообразимым количеством из 18 квинтиллионов 446 квадриллионов 744 триллионов с мелочью чисел. При всем этом число является лишь одним из возможных выражений последовательности битов, ведь с таким же успехом ее можно представить в виде акустической волны или букв (а если это ASCI-код, то это будут такие же буквы, какими вы читаете эту книжку).