Всеволод Беллюстин - Как постепенно дошли люди до настоящей арифметики с таблицей

т.-е. приводя доли въ трехразрядные классы, или же, наконецъ,

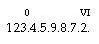
—здѣсь отмѣченъ римской цифрой VI только послѣдній разрядъ. По этой системѣ 0,000054 пишется такъ:

VI

54.

Для умноженія дается такое правило: поставь надъ послѣднимъ справа разрядомъ отвѣта такой значекъ, который равнялся бы суммѣ значковъ множимаго и множителя, стоящихъ надъ ни ми съ праваго края; всѣ остальные разряды произведенія опредѣлятся по этому крайнему разряду. Примѣръ:

VI

124 385

умножить на

IV

643

; умноживъ 124385 на 643, получимъ въ отвѣтѣ 79979555. и остается только поставить надъ послѣдней цифрой справа значекъ X, потому что VІ+IV = Х. Результатъ можно прочитать такъ: 79979555 десятаго порядка (десятыхъ скрупуловъ, по выраженік Бейера). Для дѣленія дается такое правило: сдѣлай такъ, чтобы в дѣлимомъ было столько же знаковъ, сколько и въ дѣлителѣ, или даже больше; если въ дѣлимомъ мало знаковъ, то припиши столько нулей, сколько тебѣ нужно, и это не измѣнитъ величины дроби. Потомъ произведи дѣленіе, какъ будто бы это были цѣлыя числа, и у послѣдняго разряда отвѣта поставь справа такой значекъ, который бы равнялся разности значковъ дѣлимаго и дѣлителя. Если при дѣленіи получится остатокъ, и если надо частное найти точнѣе, то можно приписывать къ дѣлимому нуль за нулемъ, сколько угодно разъ, и въ результатѣ получатся разряды, которыхъ номеръ постепенно понижается на единицу. Въ концѣ своей брошюры Бейеръ говоритъ подробно о томъ, какъ изъ десятичныхъ дробей можно получить шестидесятеричныя, и наоборотъ; также о томъ, какъ примѣнять десятичныя дроби къ рѣшенію задачъ.

Скоро и англійскій авторъ I. Неппиръ (Nepper) спѣшитъ подѣлиться съ своими читателями свѣдѣніями о новыхъ дробяхъ. Въ его книжкѣ (1626 г.) дробь пишется такъ: 28°6’7’’5’’’ и читается такъ: 28 цѣлыхъ 6 примъ 7 секундъ 5 терцій. Кромѣ того, разряды иногда у него раздѣляются точками; 27°:0’:5’’ и т. п. Сложеніе и вычитаніе идетъ у него обыкновеннымъ порядкомъ, такъ же, какъ и у насъ; вотъ примѣръ сложенія;

При умноженіи не считается необходимымъ, чтобы цифры одинаковыхъ разрядовъ стояли другъ подъ другомъ; надо умножать такъ. какъ будто бы это были все цѣлыя числа, и потомъ слѣдуетъ отсчитать съ правой стороны столько разрядовъ, сколько ихъ вмѣстѣ въ обоихъ производителяхъ; это будутъ скрупулы — десятичныя доли. Примѣры:

Въ первомъ примѣрѣ множимое раздроблено въ десятыя доли, множитель въ сотыя, произведеніе поэтому содержитъ 2671 цѣлую единицу, 6 десятыхъ, 9 сотыхъ и 5 тысячныхъ. Во второмъ примѣрѣ мы видимъ запятую между цѣлыми и десятыми. Введеніе ея приписывается извѣстному астроному Кеплеру (1571—1630).

Правило дѣленія слѣдующее: дѣлить надо, какъ цѣлыя числа, и кромѣ того надо вычесть изъ значка дѣлимаго значекъ дѣлителя, тогда остатокъ опредѣлитъ собой значекъ частнаго. Примѣръ: раздѣлить 5' 7" на 8° 6' 5" 6'". Рѣшеніе:

Въ ариѳметикѣ Беклера (1661) десятичныя дроби примѣняются только къ мѣрамъ длины, поверхности и объема; поэтому имъ дается названіе геометрическихъ долей. Цѣлыя отдѣляются отъ долей запятой или черточкой; кромѣ того, употребляются еще отмѣтки: для сажени 0, для фута 1, для дюйма 2 и для линіи 3; у послѣдней доли ставится значекъ, который опредѣляетъ ея разрядъ, и отдѣляется этотъ значекъ скобкой. Примѣръ: 123,6543 (4; это значитъ 123 сажени, 6 футовъ, 5 дюймовъ, 4 линіи и 3 точки. Какъ видно, Беклеръ проэктируетъ ввести десятичную зависимость между мѣрами, т. е. считать въ сажени 10 футовъ, въ футѣ 10 дюймовъ и т. д. Сочиненіе англичанина Вингата (1668) еще болѣе приблизило теорію десятичныхъ дробей къ тому виду, какой она имѣетъ сейчасъ. Онъ примѣняетъ дроби къ тригонометріи, къ вычисленію сложныхъ процентовъ и къ дѣйствіямъ съ именованными числами. Онъ хорошо видитъ всю громадную пользу, которая получилась бы для науки, если бы всѣ мѣры были приведены къ десятичной системѣ, иначе сказать всякая мѣра содержала бы въ себѣ ровно 10 слѣдующихъ низшихъ. Разряды десятичныхъ дробей идутъ, по мнѣнію Вингата, такъ же безпредѣльно, какъ и разряды цѣлыхъ чиселъ, такъ что за десятыми долями, сотыми, тысячными идутъ десятитысячныя, стотысячныя, милліонныя и т. д. до безконечности. Знаменателя десятичной дроби вполнѣ возможно не писать, если только условиться отдѣлять цѣлое число отъ десятыхъ долей точкой или запятой. Вингатъ пишетъ по нашему 285,82 или 285.82, но у него вмѣсто 0,5 встрѣчается .5 и вмѣсто 0,25 пишется .25, слѣд., цѣлыхъ онъ въ этомъ случаѣ не пишетъ. Три первыхъ дѣйствія онъ проходитъ совершенно аналогично съ нами, а для дѣленія у него взятъ такой порядокъ: къ дѣлимому можно приписать сколько угодно нулей и по-томъ произвести дѣйствіе такъ, какъ если бы это были цѣлыя числа; чтобы опредѣлить значеніе первой цифры частнаго, по которой уже можно разсчитать и всѣ остальные разряды, стоитъ только подписать дѣлителя подъ тѣми же разрядами дѣлимаго, которые были отчеркнуты для перваго дѣленія; подъ какимъ разрядомъ дѣлимаго находятся единицы дѣлителя, таковъ и будетъ высшій разрядъ частнаго. Примѣръ: 2,34 : 52,125. Дѣлимъ 23400000 на 52125 и получаемъ 448. Теперь подписываемъ 52,125 подъ 2,34 такъ, чтобы дѣлитель стоялъ подъ тѣмъ числомъ, которое на него дѣлилось въ первый разъ, именно

2,34000

52,125

и такъ какъ единицы дѣлителя оказались подъ сотыми долями дѣлимаго, то первая цифра частнаго 448, т. е. 4, выражаетъ собой сотыя доли и, слѣд., результатъ дѣйствія долженъ быть такой: 0,0448. Иногда нужно бываетъ при этомъ способѣ приписать съ лѣвой стороны дѣлимаго нѣсколько нулей, потому что иначе дѣлитель не можетъ помѣститься подъ дѣлимымъ. Примѣръ—0,0758 : 0,000064, тогда для удобства мы напишемъ такъ: 0000,0758 и выведемъ изъ этого, что при дѣленіи на 0,000064 высшій разрядъ частнаго составитъ тысячи, такъ какъ единицы дѣлителя оказались подъ тысячами дѣлимаго. И дѣйствительно, если произвести вычисленіе, то получится въ отвѣтѣ 1184,375.

Если сопоставить всѣ способы, какими писались десятичныя дроби въ математ. работахъ ХVIII вѣка, то получится всего пять видоизмѣненій, и если по нашему пишется 0,784, то у Бейера

III

784

, у Неппира 0°7'8"4'", у Вингата .784, у Беклера 784 (3 и у Валлиса 0<784.

Мы разсмотрѣли до сихъ поръ, кѣмъ и какъ было положено начало десятичнымъ дробямъ, и какіе успѣхи онѣ сдѣлали въ XVII столѣтіи. Въ слѣдующеvъ вѣкѣ, въ ХVIII-мъ, шестидесятеричныя дроби мало по малу исчезаютъ, и ихъ мѣсто занимаютъ десятичныя дроби. Напр., въ ариѳметикѣ нѣмецкаго педагога Париціуса, въ первомъ изданіи, которое вышло въ 1706 году, разсматриваются дроби шестидесятеричныя, но во второмъ изданіи этой же ариѳметики онѣ уже замѣнены десятичными. Впрочемъ Париціусъ, подобно Беклеру, примѣняетъ десятичныя дроби только къ мѣрамъ длины. Самое трудное изъ дѣйствій — дѣленіе онъ производитъ по такому правилу: надо дѣлить, какъ цѣлыя числа, а чтобы узнать номеръ разряда частнаго, надо изъ номера дѣлимаго вычесть номеръ дѣлителя. Вотъ примѣръ. 4269342 (5 : 321 (2 (согласно нашему обозначенію это было бы 42,69342 : 3,21).