Всеволод Беллюстин - Как постепенно дошли люди до настоящей арифметики с таблицей

Взиманіе процентовъ практиковалось еще въ древнія времена, но въ различныхъ государствахъ къ нему относились различно и вообще это дѣло было совершенно не урегулировано.

У римлянъ допускались только простые проценты, онн высчитывались по одному въ мѣсяцъ и выплачивались по истеченіи каждаго мѣсяца. Брать сложные проценты было у нихъ запрещено закономъ. Также и въ средніе вѣка во многихъ государствахъ сложные проценты запрещались закономъ, и тѣ, кто ихъ бралъ, считались ростовщиками и пользовались презрѣніемъ. Это были, обыкновенно, евреи. Законодатель исходилъ изъ того положенія, что если человѣкъ затрудняется простыми процентами и не можетъ вносить ихъ аккуратно въ срокъ, то безжалостно было-бы начислять на него сложные проценты. Въ ариѳметическихъ сборникахъ такія задачи попадались рѣдко, и въ условіяхъ ихъ говорилось, обыкновенно, про евреевъ. Въ русскомъ обществѣ до 18 ст. начисленіе процентовъ, очевидно, тоже не пользовалось расположеніемъ, по крайней мѣрѣ, у Магницкаго (1703 г.) очень мало задачъ на вычисленіе роста, и самое слово «процентъ» у него не употребляется.

Въ ХV—XVI стол., когда въ Западной Европѣ замѣчается особенный подъемъ торговли, всякія коммерческія вычисленія стали пользоваться вниманіемъ и среди нихъ вычисленіе сложныхъ процентовъ, но математикамъ того времени стоило большого труда рѣшать эти вопросы: не было десятичныхъ дробей и логариѳмовъ, да кромѣ того, мѣры стоимости были во всякомъ государствѣ свои, и переводить ихъ изъ одной системы въ другую считалось нелегкой операціей. Итальянскій математикъ Тарталья даетъ 4 способа вычисленія сложныхъ процентовъ: 1) опредѣляетъ наращенный капиталъ въ концѣ перваго года, затѣмъ въ концѣ второго и т. д., отвѣтъ находится при помощи тройного правила. 2) Пользуясь извѣстной алгебраической формулой aq n, но ея буквально не приводитъ. 3) Приростъ капитала выражаютъ его долей

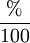
(алгебраически

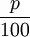
) и находятъ эту долю сперва отъ начальнаго капитала, потомъ отъ перваго наращеннаго, затѣмъ отъ второго наращеннаго и т. д.; эту долю прибавляютъ, когда нужно, къ первому капиталу, ко второму и т. д. 4) Берется произвольная сумма, обыкновенно сто рублей, и для нея находится отвѣтъ, т. е. капиталъ вмѣстѣ съ процентными деньгами, потомъ конечный отвѣтъ помножаютъ на то число, которое показываетъ, сколько сотенъ въ данномъ первоначальномъ капиталѣ. На этомъ способѣ основано и нынѣшнее пользованіе таблицами сложныхъ процентовъ.

Чтобы избѣжать трудныхъ дробей, нѣмецкій математикъ Рудольфъ (ХVІ в.) еще до введенія десятичныхъ дробей пользовался десятичными дробями. Его примѣръ такой: во что обратится сумма 375 флориновъ черезъ 10 лѣтъ по 5%? Рѣшеніе:

Въ связи съ процентами стоитъ учетъ векселей . Правило учета было извѣстно еще римлянамъ. Такъ, напр., римскій математикъ Секстъ Юлій Африканъ, писавшій свои сочиненія по ариѳметикѣ и геометріи при императорѣ Александрѣ Северѣ (222—235 г.), разсматривалъ такъ наз. interesurium, т. е. ученіе о интересахъ или процентахъ, по нашему — коммерческій учетъ векселей. Отъ римлянъ онъ перешелъ къ народамъ Западной Европы, а тамъ мы его видимъ въ XIII вѣкѣ у итальянцевъ, которые первые надумали устраивать коммерческіе банки (первые итальянскіе банки относятся къ 1200 г. по Р. X.). Самый старинный вексель, дошедшій до насъ. помѣченъ 1325 годомъ и писанъ въ Миланѣ, получить по нему въ Луккѣ. Въ XIII и XIV ст. въ Германіи встрѣчались векселя совершенно примитивной формы, но зато исключавшіе возможность всякой поддѣлки: бралась бирка, длинная палочка, и на ней графили такія зарубки, которыя могли-бы точно выражать вексельную сумму; затѣмъ эта бирка кололась по длинѣ на 2 палочки, и одна изъ нихъ вручалась должнику, другая—заимодавцу; поддѣлать такой вексель было невозможно, потому что иначе палочки другъ къ другу не подойдутъ. На учетъ векселей смотрѣли въ древніе вѣка очень косо, и дурная слава утвердилась за нимъ потому, что маклера не брезговали большими процентами; довольно обыкновеннымъ размѣромъ было 33%, а если какой маклеръ учитывалъ изъ 20%, то онъ считалсл милостивымъ.

Коммерческій учетъ называется въ настоящее время иначе учетомъ Пинкарда или Карпцова, по имени составителя и издателя таблицъ этого учета. По этому способу учета заимодавецъ остается въ убыткѣ, если учетный процентъ равенъ тому проценту, по которому брали деньги взаймы. Нашъ математическій учетъ называется иначе учетомъ Гоффмана (около 1731 г.). Третій способъ учета предложенъ Лейбницемъ. Въ немъ есть сходство съ математическимъ учетомъ, но проценты на уплачиваемую сумму начисляются сложные. Объяснимъ это алгебраически. Пусть плата будетъ X, валюта А, число процентовъ p, срокъ n лѣтъ; тогда

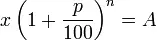
, отсюда

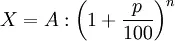
слѣдовательно, скидка или учетъ по векселю составляетъ

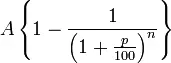
Постепенное погашеніе государственныхъ долговъ, устройство лоттерей, покупка капитала путемъ періодическихъ взносовъ, различные виды страхованія и другія банковскія и коммерческія операціи требуютъ вычисленій, основанныхъ на правилѣ сложныхъ процентовъ и на теоріи вѣроятностей. Эти вычисленія составляютъ предметъ такъ назыв. политической (коммерческой) ариѳметики. Терминъ «политическая ариѳметика» былъ въ большомъ ходу во 2-й половинѣ XVIII столѣтія. Въ новѣйшее время этотъ отдѣлъ обработанъ съ большой полнотой вѣнскими профессорами Шпитцеромъ и Габерлемъ. Въ XIX столѣтіи самое понятіе о процентѣ расширилось, благодаря введенію его въ статистику. Теперь уже отброшено старое опредѣленіе процента, какъ прибыли или убытка на сто рублей капитала, и вмѣсто того говорятъ, что процентъ просто сотая доля количества. Это опредѣленіе принимается, обыкновенно, во всѣхъ новѣйшихъ учебникахъ.

Скажемъ теперь нѣсколько словъ о правилѣ, которое у нѣмцевъ носитъ названіе «Terminrechnung», а у насъ озаглавливается „вычисленіе сроковъ платежей“. Оно примѣняется тогда, когда нѣсколько капиталовъ, отданныхъ на разные сроки и по разному числу процентовъ, надо замѣнить общимъ капиталомъ, съ тѣмъ, чтобы онъ уплачивался въ общій срокъ. Расчетъ долженъ быть основанъ на томъ, чтобы ни заимодавецъ, ни должникъ не терпѣли убытка. Примѣръ можно взять такой: я обязанъ уплатить 1000 рубл. черезъ 2 года по 5%, 2500 р. черезъ 3 г. по 4% и 3000 р. черезъ 1 годъ по 6%. Когда въ одинъ общій срокъ я могу отдать эти деньги сразу? Уже въ XVI столѣтіи итальянскими учеными было иредложено два совершенно вѣрныхъ пути для рѣшенія подобныхъ вопросовъ. Лука де-Бурго разсуждаетъ слѣдующимъ образомъ. Положимъ, что должникъ платитъ всѣ деньги въ первый срокъ; тогда онъ платитъ напрасно процентныя деньги съ остальныхъ капиталовъ, которымъ срокъ еще не настуішлъ, а именно платитъ за время между 1-мъ срокомъ и осталышми; высчитаемъ эту лишнюю сумму процентныхъ денегъ, высчитаемъ также, въ какое время эту сумму принесутъ всѣ капиталы, тогда мы и получимъ средній срокъ. Тарталья и Видманнъ пользуются нѣсколько инымъ пріемомъ, который, сравнительно съ пріемомъ Бурго, нѣсколько сокращеннѣе, именно тѣмъ, что вмѣсто прибыли вводятся произведенія капиталовъ на число дней или лѣтъ. Это и есть тотъ самый нормальный пріемъ, какой употребляется въ настоящее время.