Никола Тесла - Статьи

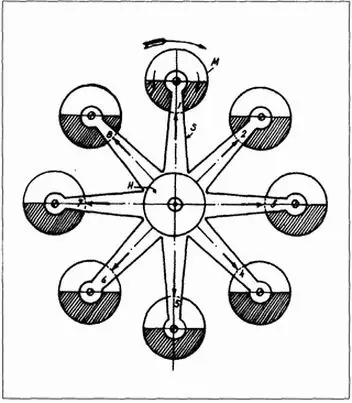
Ил. 5. Этот чертеж представляет конструкцию, состоящую из 8 шаров М, помещенных на спицы S и вращающихся вокруг центра О. Шары могут свободно вращаться на стержнях, которые могут быть закреплены. С помощью этой системы можно доказать ложность вывода об осевом вращении Луны

С этой целью обратим внимание на иллюстрацию 5, представляющую систему, состоящую из восьми шаров М , которые укреплены на спицах радиально исходящих из ступицы H , вращающейся вокруг центральной оси О , предположим, на подшипниках качения. Это устройство подобно представленному выше, за исключением того, что шары не имеют жесткого соединения со спицами, а насажены на винтовые стержни S , которые обычно свободно вращаются, но могут быть закреплены, с тем чтобы позволить и шарам, и осям свободно вращаться и жестко закрепляться, когда это будет необходимо. Для облегчения наблюдения на спицы нанесены радиальные обозначения, а нижняя часть шаров заштрихована. Изначально допустим, что чертеж изображает состояние покоя, при этом шары могут свободно вращаться, не встречая помех в виде трения, и пусть системе будет сообщена угловая скорость ω = 2π n движения по часовой стрелке, как показывает длинная жирная стрелка. Представим себе шар М , при этом его последовательные положения 1, 2, 3–8 в пространстве, а также относительно спицы будут именно такими, какими они изображены на чертеже, тогда анализ этого графика делает очевидным тот факт, что шар, перемещаясь с угловой скоростью ω вокруг О в направлении часовой стрелки, вращается относительно своей оси с той же угловой скоростью, но в противоположном направлении, указанном пунктирной стрелкой. Объединенный результат этих двух движений есть такое поступательное движение шара, что все частицы приводятся в движение с одной и той же скоростью V , которая равна скорости его центра тяжести. В этом случае, при условии, что нет абсолютно никакого трения, кинетическая энергия каждого шара будет определяться произведением ½ MV ², и не приблизительно, а с математической точностью. В случае, когда оси плотно закреплены и шары жестко зафиксированы на спицах, такое вращательное движение относительно осей становится физически невозможным, и тогда выясняется, что кинетическая энергия каждого шара возрастает, при этом прирост абсолютно равен энергии вращения шара на своей оси.

Этот факт, подкрепленный и теоретически, и экспериментально, является основой всеобщей убежденности, что вращающееся тело — в данном варианте шар М , обращая всегда одну и ту же сторону к центру движения, как ни странно , вращается на своей оси в том направлении, которое обозначено короткой сплошной стрелкой. Но вращения не происходит, хотя, на первый взгляд, кажется, что оно есть. Заблуждение выявится в ходе дальнейшего исследования.

Для начала обратите внимание на то, что, когда масса, скажем, якорь электромотора, вращающийся с угловой скоростью ω, реверсирует, его скорость равна -ω, а разность ω — (-ω) = 2ω. Тогда, если шар зафиксировать на спице, разность угловой скорости составит лишь ω: следовательно, ему должна быть сообщена дополнительная скорость ω, чтобы вызвать вращение шара на собственной оси по часовой стрелке в истинном значении слова. Тогда кинетическая энергия была бы равна сумме энергий поступательного и осевого движений, не просто в абстрактном математическом значении, но в качестве физического явления. Я в полной мере осознаю, что, согласно широко распространенному мнению, если шар не зафиксирован на стержне, он вообще не поворачивается на своей оси, он лишь вращается с угловой скоростью всей конструкции, будучи жестко закрепленным на той же оси, но истина будет очевидна после более детального изучения этого вида движения.

Пусть система вращается, как было принято и проиллюстрировано вначале, когда шары не закреплены на стержнях, и пусть стержни постепенно закрепляются, вызывая трение, которое медленно уменьшает и, в конце концов, препятствует скольжению. На начальном этапе все части каждого шара перемещались со скоростью центра тяжести, но так как подшипниковое сопротивление всё более и более заявляет о себе, поступательная скорость частиц, находящихся ближе к оси О , будет убывать , в то время как таковая диаметрально противолежащих частиц будет возрастать , пока не будут достигнуты максимальные значения этих изменений, когда шары прочно закреплены. В этом процессе мы, таким образом, отбираем массы у частиц, находящихся ближе к центру движения, и тем самым кинетическую энергию поступательного движения , в то же время добавляем к энергии тех частиц, которые находятся дальше и, очевидно, что прирост окажется бóльшим, чем потеря, так что фактическая скорость каждого шара в целом возрастет. Только за счет этого мы имеем возрастание кинетической энергии системы, а не по причине осевого вращения шаров. Энергия Е каждого из них есть исключительно энергия поступательного движения с фактической скоростью V e, определенной выше, так что Е = ½ MV e ². Осевые вращения шара в любом из двух направлений лишь кажущиеся; они не имеют какой бы то ни было реальной основы и не требуют никакого механического усилия. Только в том случае, когда действует независимая внешняя сила, чтобы вращать ротативное тело на его оси, эта энергия проявит себя.

В этой связи следует указать, что при истинном осевом вращении неподвижно закрепленной и однородной массы все симметрично расположенные частицы вносят равный вклад в количество движения, что в данном случае не имеет места. Тот факт, что не существует даже малейшей тенденции к такому движению, может быть без труда доказан.

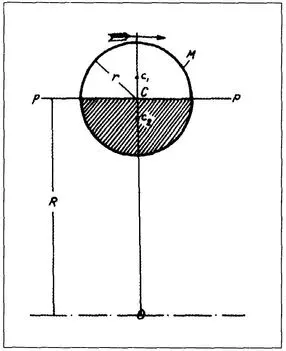
Ил. 6. Чертеж, представляющий шар с массой М и радиусом r, вращающийся вокруг центра О, служит для теоретического исследования движения Луны

Для этого я сошлюсь на иллюстрацию 6, где представлен шар М с радиусом r и с центром С , находящимся на расстоянии R от оси О ; шар разделен на две равные части тангенциальной плоскостью pp , как показано, при этом нижняя часть сферы заштрихована для распознавания. Кинетическая энергия шара, при условии, что он совершает n оборотов в секунду вокруг О , определяется согласно первому варианту выражения как E = ½ MV e ² = ½ M (2π R gn )², где M — масса, a R g — радиус вращательного движения. Но, как говорилось в пояснении к иллюстрации 4, мы также имеем выражение Е = ½ MV ² + ½ I eω², где V = 2π Rn есть скорость центра тяжести С , а I e — момент инерции шара, находящегося в окрестности параллельной оси, проходящей через С и равный 2/ 5 Мi ², так что Е = ½М(2π Rn )² + 1/ 5 Мr ²(2π n )². Ни одно из этих двух выражений для E не характеризует фактическое состояние тела, но первое, конечно, предпочтительнее, так как передает в сущности идею единого движения вместо двух, из которых одно не имеет основы для существования. Я берусь прежде всего доказать, что не существует вращающего момента, или вращательного усилия, вокруг центра С, и что кинетическая энергия воображаемого осевого вращения шара в математическом смысле равна нулю. Это приводит к необходимости считать две половины, разделенные тангенциальной плоскостью pp, полностью независимыми одна от другой. Пусть с 1и с 2будут их центрами тяжести, тогда С c1= С c2= 3/ 8 r . Чтобы определить кинетическую энергию полусфер, мы должны найти их радиусы движения по окружности, что можно сделать, определив моменты инерции I c1и I с2в окрестности параллельной оси, проходящей через с 1и с 2. Можно избежать сложных вычислений, если помнить, что момент инерции любой из полусфер в окрестности оси, проходящей через С , выражается формулой Ic = ½ × 2/ 5 Mr ² = 1/ 5 Mr ², и поскольку М = 2 т , то I c= 2/ 5 mr ². Это можно выразить через моменты I c1и I с2, а именно: I c= I с1+ m ( 3/ 8 r )² = I c2+ m ( 3/ 8 r )². Следовательно, I c1= I c2= I c— m ( 3/ 8 r )² = 2/ 5 mr ² — 9/ 64 mr ² = 83/ 320 mr ². Следуя этому же правилу, можно найти моменты инерции полусфер в окрестности оси, проходящей через центр движения О .